标签：
作者 白宁超
2015年8月15日22:51:38
摘要：本文继统计学几何分布、二项分布、泊松分布研究的深入，基于各种分布基础概念和核心知识介绍之后。就各种分布的实现和真实环境下应用方是目的。在进行一系列相互独立实验，每次既有成功，又有失败的可能，且单次实验成功概率相等。在一系列试验中求成功的次数。这种情况下适用于本算法。本算法中在n次伯努利试验中：试验n次得到r次成功的概率、二项分布的期望、二项分布方差的具体实现。
在进行一系列相互独立实验，每次既有成功，又有失败的可能，且单次实验成功概率相等。在一系列试验中求成功的次数。这种情况下适用于本算法。
本算法中在n次伯努利试验中：试验n次得到r次成功的概率、二项分布的期望、二项分布方差的具体实现。
在相互独立事件中，每道题答对概率为p，答错概率为q。在n个问题中答对r个问题的概率为：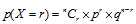 
这类问题称之为二项分布。表达式为：X~B(n,p)
n：表示总试验次数
X：表示n次独立试验获取成功的次数
p：表示独立试验成功的概率
q：表示独立试验失败的概率
假设成功概率为p，失败概率为q，n次伯努利试验中，试验次数为r的前提下满足：
1、第r次试验第一次成功：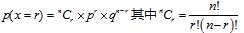 
2、期望：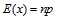
3、方差：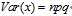 
案例描述：一次竞猜游戏中共有5个问题，每一题答对的概率为0.25，假设每一次答题都是独立事件。
案例定义：答题者单次独立成功概率为0.25，失败概率为0.75，知道总共5道题目，即可求出相关答对次数。
n：表示总试验次数，n=5。
X：表示n次独立试验获取成功的次数,X=r(第r次)。
p：表示独立试验成功的概率，p=0.25。
q：表示独立试验失败的概率, q=1-p=0.75。
案例计算：假设成功概率为p=0.25，失败概率为q=1-p，n次伯努利试验中，总共5道题目的前提下满足：
1、答对两道题的概率：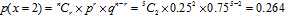
2、一题答不对的概率：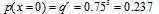 
4、期望：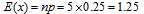
5、方差：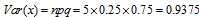 
优点：在试验次数一定，求成功次数时，几何分布显示不适合的情况下，给予这类问题二项分布能更好的解决。
缺点：但是面对试验次数不固定，发生事件概率的情况下，显然几何分布与二项分布都不能解决，这里也体现出泊松分布的优势。
n次试验在相同条件下进行，各个观察单位的结果独立，且只能具有相互对立的一种结果，目的：第N次试验中成功多少次。
在非独立试验情况，或者独立试验情况下获取第一次成功的概率，不适用二项分布。
本算法适用于double数据类型，默认保留两位小数，可以自行设定保留位数。
* @param n int，表示总的独立事件
* @param r int，表示发生r次
* @param p double，表示成功的概率
方法RSucess中：
* @param q double，表示失败的概率即1-p
* @param ncr double，表示成功的组合次数
* @return PX double型保留两位小数，需要n次试验r成功的概率
* @return EX double型保留两位小数，二项分布的期望
* @return VX double型保留两位小数，二项分布的方差
异常1：输入数据不合法，如：要求输入double数据，输入字母。
异常2：输入数据特别大，超越计算能力
误差1：计算组合结果数据保留位数，截取字符，存在一定细微误差
误差2：保留小数位数造成不精确
异常1：解决，输入不合法给予提示。
异常2：解决，进行异常捕获
误差1：解决，尽量中间计算过程不保留小数位，减小误差影响
误差2：解决，进行小数点位数自定义保留封装，根据具体精度进行设置。
类源码：见源程序：Distributes. src. DistTools. BinoDist
本算法中在n次伯努利试验中：试验n次r次成功的概率、二项分布的期望、二项分布方差的具体实现。
见源程序：Distributes. src. DistTools. BinoDist
BinoDist.java 下包含如下方法：
RSuccess(int n,int r,double p,double q) //试验n次独立试验，r次成功的概率
Expectation(int n,double p) //二项分布的期望
Variance(int n,double p,double q) //二项分布方差
调用封装方法：
NumFormat.java 下如下方法：
DecFormat(int n,double num) //对num数值保留位数n的自行设置
factorial(int num) //对num数值求阶乘
类的注释如下：
package DistTools; /** * * @(#)GeoDist.java * @Description:描述：本算法中在n次伯努利试验中：试验n次得到r次成功的概率、二项分布的期望、二项分布方差的具体实现。 * @Definitions:定义：在相互独立事件中，每道题答对概率为p，答错概率为q。在n个问题中答对r个问题的概率为：P(X=r)=C_n_r*P^r*q^(n-r)这类问题称之为二项分布。表达式为：X~B(n,p) * @Explanation:符号解释：n：表示总试验次数;X：表示n次独立试验获取成功的次数;p：表示独立试验成功的概率;q：表示独立试验失败的概率 * @Comments:条件：在进行一系列相互独立实验，每次既有成功，又有失败的可能，且单次实验成功概率相等。在一系列试验中求成功的次数。这种情况下适用于本算法。 * @优点:在试验次数一定，求成功次数时，几何分布显示不适合的情况下，给予这类问题二项分布能更好的解决 * @缺点:但是面对试验次数不固定，发生事件概率的情况下，显然几何分布与二项分布都不能解决，这里也体现出泊松分布的优势。 * @适用场景:n次试验在相同条件下进行，各个观察单位的结果独立，且只能具有相互对立的一种结果，目的：第N次试验中成功多少次。 * @不适用场景:在非独立试验情况，或者独立试验情况下获取第一次成功的概率，不适用二项分布。 * @输入/出参数:见具体方法 * @异常/误差: * 异常1：输入数据不合法，如：要求输入double数据，输入字母。 * 异常2：输入数据特别大，超越计算能力 * 误差1：计算组合结果数据保留位数，截取字符，存在一定细微误差 * 误差2：保留小数位数造成不精确 * 解决： * 异常1:输入不合法给予提示。 * 异常2：进行异常捕获 * 误差1：尽量中间计算过程不保留小数位，减小误差影响。 * 误差2：进行小数点位数自定义保留封装，根据具体精度进行设置。 * @Create Date： 2015年8月3日20:29:13 * @since JDK1.6 s * @author Bai ningchao */
方法一：第一次成功概率的方法注释以及实现
注释：
/**
* 在n次伯努利试验中，在n次独立的伯努利试验发生r次的概率为
* P(X=r)=C_n_r*p^{r}*q^{n-r}且C_n_r=n!/(r!*(n-r)!)
* @param n int，表示总的独立事件
* @param r int，表示发生r次
* @param p double型保留一位小数，表示成功的概率
* @return PX double型保留两位小数，5道题目答对两道题的概率
*/
代码：
public static double RSucess(int n,int r,double p) { double PX=0; double q=1-p; //表示失败的概率即1-p try { //根据C_n_r=n!/r!*(n-r)!求n个事件中r次的组合 double ncr=NumFormat.factorial(n)/(NumFormat.factorial(r)*NumFormat.factorial(n-r)); PX=ncr*(Math.pow(p, r))*(Math.pow(q, (double)(n-r)));//根据公式P(X=r)=C_n_r*p^{r}*q^{n-r}求解二项分布的概率 PX=NumFormat.DecFormat(4,PX); System.out.println(">> 5道题目答对两道题的概率：" + PX); } catch(Exception e) { System.out.println(">> 错误信息描述："+e.getMessage()); } return PX; }
方法二：二项分布的期望方法注释以及实现
注释：
/**
* 在n次伯努利试验中，二项分布的期望公式：E(X)=np
* @param n int型，表示试验的次数
* @param p double型保留一位小数，表示成功的概率
* @return EX double型保留两位小数，二项分布的期望
*/
代码：
public static double Expectation(int n,double p)
{
double EX=0;
try
{
EX= Double.valueOf(n)*p;//根据二项分布的期望公式E(X)=np 求期望
EX=NumFormat.DecFormat(4,EX);
System.out.println(">> 二项分布期望：" + EX);
}
catch(Exception e)
{
System.out.println(">> 错误信息描述："+e.getMessage());
}
return EX;
}
方法三：二项分布的方差方法注释以及实现
注释：
/**
* 在n次伯努利试验中，二项分布的方差公式：Var(X)=npq
* @param n int型，表示试验的次数
* @param p double型保留一位小数，表示成功的概率
* @param q double型保留一位小数，表示失败的概率即1-p
* @return VX double型保留两位小数，二项分布的方差
*/
代码：
public static double Variance(int n,double p)
{
double VX=0;
double q=1-p; //表示失败的概率即1-p
try
{
VX= Double.valueOf(n)*p*q;//根据二项分布的方差公式Var(X)=npq 求方差
VX=NumFormat.DecFormat(4,VX);
System.out.println(">> 二项分布的方差：" + VX);
}
catch(Exception e)
{
System.out.println(">> 错误信息描述："+e.getMessage());
}
return VX;
}
public static void main(String[] args) throws Exception {
//PX是返回5道题目答对两道题的概率 0.2637
BinoDist.RSucess(5, 2, 0.25); //参数1:总共题目个数n，参数2:答对题目个数r，参数3:独立事件成功的概率p
//EX是二项分布的期望 1.25
BinoDist.Expectation(5, 0.25); //实参1:独立事件成功的概率p
//VX是二项分布的方差 0.9375
BinoDist.Variance(5, 0.25); //实参1:独立事件成功的概率p
}
标签：
原文地址：http://www.cnblogs.com/baiboy/p/tjx721.html
