标签:
/**
* 冒泡排序
* @param arr
*/
public void bubbleSort(int[] arr){
for (int out = arr.length-1; out >1 ; out--) {
for (int in = 0; in < out; in++) {
if(arr[in] > arr[in+1]){
swap(arr, in, in+1);
}
}
}
}
private void swap(int[] arr, int aIndex, int bIndex){
int temp = arr[aIndex];
arr[aIndex] = arr[bIndex];
arr[bIndex] = temp;
}
时间复杂度:O(n*n)
特点:改进了冒泡排序,将交换次数从O(n*n)减少到O(n),但是比较次数仍为O(n*n)
/** * 选择排序 * @param arr */ public void selectSort(int[] arr){ int minIndex; for (int out = 0; out < arr.length -1; out++) { minIndex = out; for (int in = out+1; in < arr.length; in++) { if(arr[minIndex] > arr[in]){ minIndex = in; } } swap(arr, out, minIndex); } } private void swap(int[] arr, int aIndex, int bIndex){ int temp = arr[aIndex]; arr[aIndex] = arr[bIndex]; arr[bIndex] = temp; }
时间复杂度:O(n*n)
特点:虽然时间复杂度仍为O(n*n),但是一般情况下,要比冒泡排序快一倍,比选择排序还要快点。如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的数目。
/**
* 插入排序
* @param arr
*/
public void insertSort(int[] arr, int left, int right){
int in;
int markedNum;
for (int out = left+1; out <= right; out++) {
in = out;
markedNum = arr[out];
while(in > left && arr[in] >= markedNum){
arr[in]= arr[in-1];
in--;
}
arr[in] = markedNum;
}
}
时间复杂度:O(n log n)
/** * 归并排序 * @param arr */ public void mergeSort(int[] arr, int low, int high){ if(low == high) { return; }else{ int mid = (low + high)/2; mergeSort(arr,low,mid); mergeSort(arr,mid+1,high); merge(arr,high,mid,low); } } private void merge(int[] arr, int high, int mid, int low){ int arrLen = arr.length; int[] newArr = new int[arrLen]; int lowFlag= low; int highFlag = mid+1; int i = 0; int totalNum = high - low +1; while (lowFlag <= mid && highFlag <= high){ if(arr[lowFlag] < arr[highFlag]){ newArr[i++] = arr[lowFlag]; lowFlag++; }else{ newArr[i++] = arr[highFlag]; highFlag++; } } while(lowFlag <= mid){ newArr[i++] = newArr[lowFlag++]; } while(highFlag <= high){ newArr[i++] = newArr[highFlag++]; } for (int j = 0; j <totalNum; j++) { arr[j+low] = newArr[j]; } }
时间复杂度:大约为
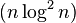
特点:希尔排序是直接插入排序算法的一种改进,减少了其复制的次数,速度要快很多。 原因是,当n值很大时数据每一趟排序需要的个数很少,但数据项的距离很长。当n值减小时每一趟需要和动的数据增多,此时已经接近于它们排序后的最终位置。
/**
* 希尔排序
* @param arr
*/
public void shellSort(int[] arr){
int h = 1;
int arrLen = arr.length;
int temp;
int in;
while(h < arrLen/3){
h = h * 3 + 1;
}
while(h > 0){
for (int i = h; i < arrLen; i++) {
temp = arr[h];
in = i;
while(in>h-1 && arr[in-h] >= temp){
arr[in] = arr[in - h];
in -=h;
}
arr[in] = temp;
}
h = (h-1)/3;
}
}
时间复杂度:O(N*logN)
/**
* 快速排序
* @param arr
* @param left
* @param right
*/
public void quickSort(int[] arr, int left, int right){
int size = right - left + 1;
if(size < 10){
insertSort(arr, left, right);
}else{
if(left >= right){
return;
}else{
int mid = midOf3(arr, left, right);
int partition = partitionIt(arr, left, right, mid);
quickSort(arr, left, partition-1);
quickSort(arr, partition + 1, right);
}
}
}
private int midOf3(int[] arr, int left, int right){
int mid = (left + right)/2;
if(arr[left] > arr[mid]){
swap(arr, left, mid);
}
if(arr[left] > arr[right]){
swap(arr, left, right);
}
if(arr[mid] > arr[right]) {
swap(arr, mid, right);
}
swap(arr, mid, right-1);
return arr[right -1];
}
private int partitionIt(int[] arr, int left, int right, int pivot){
int rightFlag = right;
int leftFlag = left-1;
while(true){
while(rightFlag > 0 && arr[rightFlag --] > pivot);
while(arr[leftFlag ++ ] < pivot);
if(leftFlag >= rightFlag) {
break;
}else{
swap(arr, leftFlag, rightFlag);
}
}
swap(arr, leftFlag, right);
return leftFlag;
}
标签:
原文地址:http://www.cnblogs.com/happySmily/p/4734317.html