标签:
快速求正整数次幂,当然不能直接死乘。举个例子:
3 ^ 999 = 3 * 3 * 3 * … * 3
直接乘要做998次乘法。但事实上可以这样做,先求出2^k次幂:
3 ^ 2 = 3 * 3
3 ^ 4 = (3 ^ 2) * (3 ^ 2)
3 ^ 8 = (3 ^ 4) * (3 ^ 4)
3 ^ 16 = (3 ^ 8) * (3 ^ 8)
3 ^ 32 = (3 ^ 16) * (3 ^ 16)
3 ^ 64 = (3 ^ 32) * (3 ^ 32)
3 ^ 128 = (3 ^ 64) * (3 ^ 64)
3 ^ 256 = (3 ^ 128) * (3 ^ 128)
3 ^ 512 = (3 ^ 256) * (3 ^ 256)
再相乘:
3 ^ 999 = 3 ^ (512 + 256 + 128 + 64 + 32 + 4 + 2 + 1)
= (3 ^ 512) * (3 ^ 256) * (3 ^ 128) * (3 ^ 64) * (3 ^ 32) * (3 ^ 4) * (3 ^ 2) * 3
这样只要做16次乘法。即使加上一些辅助的存储和运算,也比直接乘高效得多(尤其如果这里底数是成百上千位的大数字的话)。
我们发现,把999转为2进制数:1111100111,其各位就是要乘的数。这提示我们利用求二进制位的算法(其中mod是模运算):
所以就可以写出下面的代码:
double Pow(double x, int n) { double result = 1; while (n) { if (n & 1) // 等价于 if (n % 2 != 0) result *= x; n >>= 1; x *= x; } return result; }
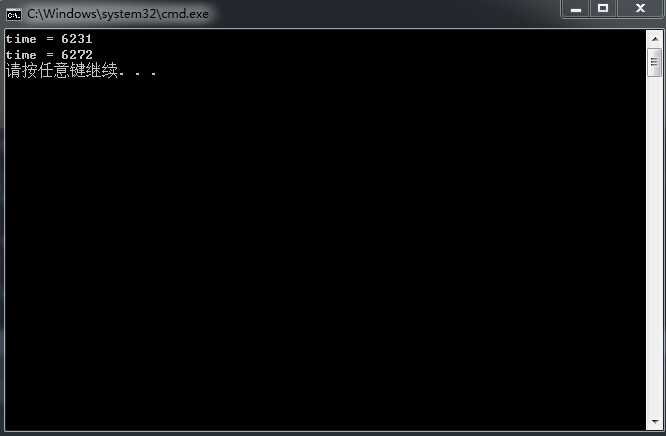
最后测试一下与C语言标准库函数中的pow函数的比较:
#include <stdio.h> #include <math.h> #include <time.h> using namespace std; #define COUNT 100000000 double Pow(double x, int n) { double result = 1; while (n) { if (n & 1) result *= x; n >>= 1; x *= x; } return result; } int main() { int start, end; start = clock(); for (int i = 0; i < COUNT; i++) Pow(2.0, 100); end = clock(); printf("time = %d\n", (end - start)); start = clock(); for (int i = 0; i < COUNT; i++) pow(2.0, 100.0); end = clock(); printf("time = %d\n", (end - start)); return 0; }
最终的结果是差不多的
标签:
原文地址:http://www.cnblogs.com/XiangfeiAi/p/4738087.html