标签：
一步了解
常见的梯度下降法主要有两种：（1）批量梯度下降法 （2）随机梯度下降法
为预测值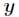
，要拟合的函数设为
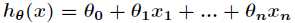，那么误差准则函数为
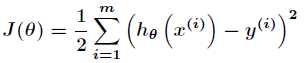
这是典型的线性回归问题，现在的目的是使得这个误差准则函数的值最小化，可以用如下两种梯度下降法。
（1）批量梯度下降法
批量梯度下降法需要把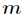
个样本全部带入计算，迭代一次计算量为
，先对误差准则函数求偏导
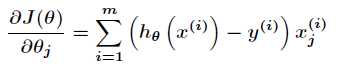
所以进一步得到批量梯度下降的迭代式为
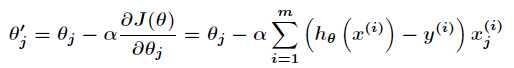
可以看出批量梯度下降法得到的是一个全局最优解，但是每迭代一步要用到训练集所有的数据，如果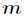
很大那么计算量会很大，相应速度会很慢。所以针对这种不足，又引入了另一种方法：随机梯度下降法。
（2）随机梯度下降法
上面的批量梯度下降法是将所有的样本都带入计算，而随机梯度下降法每次迭代是带入单个样本，迭代
，当样本数总数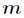
很大的时候，随机梯度下降法迭代一次的速度要远远小于梯度下降
代公式如下
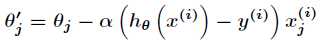
可以看出随机梯度下降法是最小化单个样本的误差准则函数，虽然每次迭代误差准则函数都不一定是向
着全局最优方向，但是大的整体方向是向着全局最优方向的，最终得到的结果往往在全局最优解附近。
对于上述线性回归问题，来分析一下这个误差准则函数的性质，首先对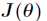
求二阶偏导数，得到
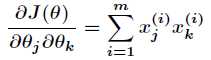
即得到Hessian矩阵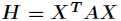
，中间的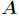
是一个单位矩阵且正定，所以Hessian矩阵正定。进而推出
误差准则函数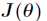
是单峰函数，那么通过梯度下降法得到的最优解也就是全局最优解。当然如果一个函数有
多个峰，那么通过梯度下降得到的可能不是全局最优解。
其实梯度下降法，在使用的时候无非是考虑到两个方面：一是方向，二是步长。方向决定是否走在最优化的道
路上，而步长决定了要多久才能到达最优的地方。对于第一方面，就是求梯度，多元函数求相应变量的偏导数；
回震荡，所以步长选择比较关键。
标签：
原文地址：http://www.cnblogs.com/wft1990/p/4741800.html
