标签:
输入一个数组,利用一组二叉树的操作使其变成有序的数组,就是堆排序
堆排序利用的是二叉树的思想,操作对象是数组,所以数组需要在逻辑上映射到二叉树上,由于数组的下标是连续的,而二叉树中只有完全二叉树和满二叉树是连续的,所以将数组元素逐个映射到完全二叉树上,然后配备一系列的操作即可。例如数组data[]={9,6,5,4,3,2,1,7},映射到完全二叉树上如下图所示。
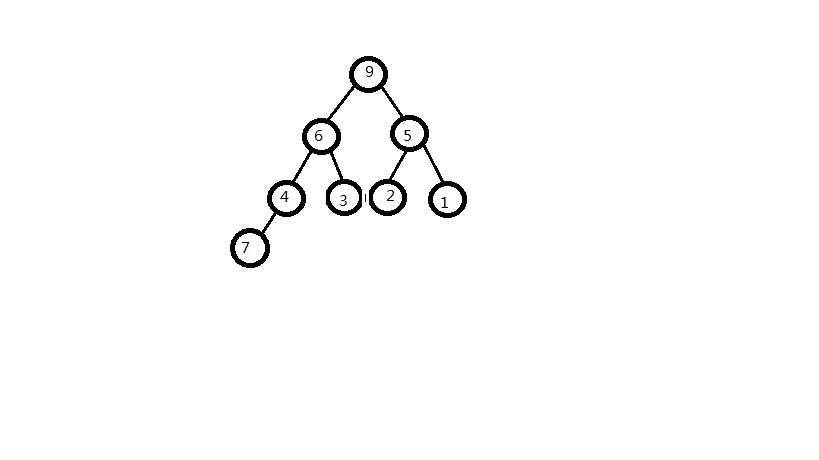
还是用上面的data数组作为输入数组,映射到完全二叉树如上图所示,怎么利用二叉树的性质,才能使得数组有序呢?首先需要取得二叉树中的最大值(或者最小值),显然需要建立最大堆,取得二叉树的根节点即最大值,放置在数组中最后一个位置上,再将二叉树中的最后一个节点放置在根节点上,调整堆使其变成最大堆,取最大值放在数组中倒数第二个位置上.......这样的调整需要n-1次,数组有序。
总结上述过程,堆排序需要三个步骤:
A、根据输入数组,建立最大堆
B、保持最大堆的性质
C、循环n-1次,找到(n-1)堆中每个堆的最大值并放置在数组中,数组有序
首先,这三个过程中,我觉得最重要的是保持最大的堆的性质,其实就是在二叉树中不断使元素下行,直至满足最大堆的要求。需要知道,数组中下标为i的元素,它的左孩子下标是2i+1,右孩子的下标是2i+2,保持最大堆函数的伪代码如下所示(伪代码--算法导论上第75页)。
1 MAX_HEAPFY(A,i) 2 l=LEFT(i) //l=2*i+1 3 r=LEFT(i) //r=2*i+2 4 if(l<=heap_size(A)&&A[i]<A[l]) 5 largest=l; //largest记录最大值下标 6 else 7 largest=i; 8 if(r<=heap_size(A)&&A[largest]<A[r]) 9 largest=r; 10 if(i!=largest) //如果largest不是i,则说明现在不是最大堆,需要调整 11 exchange(A[i],A[largest]) //使下标i上的元素具有最大值,然后继续向下调整 12 MAX_HEAP(A,largest)
其次,在完成max_heapfy后,接下来的工作就是根据输入数组建立最大堆,由max_heapfy知道,函数的参数i代表的是根节点的下标,在一个长度为len的数组中,下标最大的根节点的下标是(i/2),我们可以从下到上依次调整形成最大堆,这个过程就是建立最大堆的过程,与MAX_HEAPFY调整函数不同,这个过程是一个元素上行的过程。建堆的伪代码如下所示。
1 BUILD_MAX_HEAP(A) 2 heap_size(A)=length(A) 3 for(int i=length(A)/2;i>=0;i--) 4 MAX_HEAPFY(A,i)
最后,完成以上两步后,取最大堆的堆顶元素,放置在数组中对应的位置上,不断循环,这个过程需要进行length(A)-1次,数组便可有序。这个过程的伪代码如下所示。
1 HEAPSORT(A) 2 BUILD_MAX_HEAP(A) 3 for(int i=length(A)-1;i>=1;i--) 4 exchange(A[0],A[i]); 5 heap_size(A)=heap_size(A)-1 6 MAX_HEAPFY(A,0);
由上述说明,堆排序的输入数组和一个完全二叉树对应,假设数组大小时N,则二叉树的高度是lgN,所以保持最大堆性质的调整操作所需要的时间复杂度是O(lgN),而建立一个最大堆的时间复杂度是O(n)(这个结论的推导在算法导论的第78页),最后的排序时间复杂度为(n-1)*lgN
所以,这个堆排序的时间复杂度是T(N)=O(N)+(n-1)*lgN,T(N)=O(NlgN),需要说明的一点是堆排序对于输入的数据的随机性没有特别的要求,也就是说,在最好、最坏和平均情况下,堆排序的时间复杂度都是O(nlgn)
堆排序不是一种稳定的排序方法。
附上堆排序的代码(codeblocks已通过):
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <malloc.h> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 void max_heapfy(int data[],int heap_size,int i){ 8 int left=2*i+1; 9 int right=2*i+2; 10 int largest; 11 if(left<heap_size&&data[left]>data[i]) 12 largest=left; 13 else 14 largest=i; 15 if(right<heap_size&&data[right]>data[largest]) 16 largest=right; 17 if(largest!=i){ 18 swap(data[i],data[largest]); 19 max_heapfy(data,heap_size,largest); 20 } 21 } 22 void build_heap(int data[],int length){ 23 for(int i=length/2-1;i>=0;i--) 24 max_heapfy(data,length,i); 25 } 26 void heap_sort(int data[],int length){ 27 if(data==NULL||length<=0) 28 return ; 29 build_heap(data,length); 30 int heap_size=length; 31 for(int i=length-1;i!=0;i--){ 32 swap(data[i],data[0]); 33 heap_size-=1; 34 max_heapfy(data,heap_size,0); 35 } 36 } 37 int main(){ 38 int data[]={6,5,4,9,7,8,2,1,3,5}; 39 int length=sizeof(data)/sizeof(int); 40 heap_sort(data,length); 41 for(int i=0;i<length;i++) 42 cout << data[i] << " "; 43 return 0; 44 }
标签:
原文地址:http://www.cnblogs.com/sjinsa/p/4743563.html