标签:
1、关于时间复杂度
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,它考察当输入值大小趋近无穷时的情况。举例,如果一个算法对于任何大小为 的输入,它至多需要
的输入,它至多需要 的时间运行完毕,那么它的渐近时间复杂度是
的时间运行完毕,那么它的渐近时间复杂度是 。
。
2、常用的时间复杂度列表
| 名称 | 复杂度类 | 运行时间( ) ) | 运行时间举例 | 算法举例 |
|---|---|---|---|---|
| 常数时间 |  |
10 | 判断一个二进制数的奇偶 | |
| 反阿克曼时间 |  |
并查集的单个操作的平摊时间 | ||
| 迭代对数时间 | 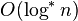 |
en:Cole-Vishkin algorithm | ||
| 对数对数时间 |  |
有界优先队列的单个操作[1] | ||
| 对数时间 | DLOGTIME |  |
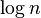 , , |
二分搜索 |
| 幂对数时间 |  |
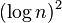 |
||
| (小于1次)幂时间 |  ,其中 ,其中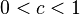 |
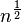 , , |
K-d树的搜索操作 | |
| 线性时间 |  |
 |
无序数组的搜索 | |
| 线性迭代对数时间 |  |
Raimund Seidel的三角分割多边形算法 | ||
| 线性对数时间 |  |
 , , |
最快的比较排序 | |
| 二次时间 |  |
 |
冒泡排序、插入排序 | |
| 三次时间 |  |
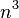 |
矩阵乘法的基本实现,计算部分相关性 | |
| 多项式时间 | P | 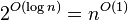 |
 , , , , |
线性规划中的en:Karmarkar‘s algorithm,AKS质数测试 |
| 准多项式时间 | QP |  |
关于有向斯坦纳树问题最著名的 近似算法 近似算法 |
|
| 次指数时间(第一定义) | SUBEXP | 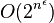 ,对任意的ε > 0 ,对任意的ε > 0 |
 |
Assuming complexity theoretic conjectures, BPP is contained in SUBEXP.[2] |
| 次指数时间(第二定义) | 2o(n) | 2n1/3 | Best-known algorithm for integer factorization and graph isomorphism | |
| 指数时间 | E | 2O(n) | 1.1n, 10n | 使用动态规划解决旅行推销员问题 |
| 阶乘时间 | O(n!) | n! | 通过暴力搜索解决旅行推销员问题 | |
| 指数时间 | EXPTIME | 2poly(n) | 2n, 2n2 | |
| 双重指数时间 | 2-EXPTIME | 22poly(n) | 22n | Deciding the truth of a given statement in Presburger arithmetic |
3、复杂度举例
* O(1) 常数级复杂度,也就是说程序运行的时间与需要处理的数据大小无关。通常把比较大小、加减乘除等简单的运算都当做常数级复杂度。 值得注意的是,在处理大数(二进制下数据长度超过32位或者十进制下超过8位)时,将加减乘除等运算当做常数复杂度不再适用。
* O(log n) 将一个10进制整数转化为2进制整数
* O(n):判断一个元素是否属于一个大小为n的集合/列表;找出n个数中的最大值;
* O(n * log n) 快速排序法
* O(n^2) 最直白的两两比较然后排序方法,需要n*(n-1)/2次比较,所以是O(n^2)级。
* O(2^n) 列出所有长度为n的0,1字符串之类的穷举计算
* O(n!) 列出n个元素的全排列之类的穷举计算
4、对数时间
若算法的T(n) = O(log n),则称其具有对数时间。由于计算机使用二进制的记数系统,对数常常以2为底(即log2 n,有时写作lg n)。然而,由对数的换底公式,loga n和logb n只有一个常数因子不同,这个因子在大O记法中被丢弃。因此记作O(log n),而不论对数的底是多少,是对数时间算法的标准记法。
常见的具有对数时间的算法有二叉树的相关操作和二分搜索。
对数时间的算法是非常有效的,因为每增加一个输入,其所需要的额外计算时间会变小。
递归地将字符串砍半并且输出是这个类别函数的一个简单例子。它需要O(log n)的时间因为每次输出之前我们都将字符串砍半。 这意味着,如果我们想增加输出的次数,我们需要将字符串长度加倍。
// 递归输出一个字符串的右半部分 var right = function(str) { var length = str.length; // 辅助函数 var help = function(index) { // 递归情况:输出右半部分 if(index < length){ // 输出从index到数组末尾的部分 console.log(str.substring(index, length)); // 递归调用:调用辅助函数,将右半部分作为参数传入 help(Math.ceil((length + index)/2)); } // 基本情况:什么也不做 } help(0); }
本文参考的维基百科中对“时间复杂度”的描述。
标签:
原文地址:http://www.cnblogs.com/suiying/p/4746619.html