标签:
余数专题
1. 取模性质
加法 (a + b) % p = a % p + b % p;
减法 (a - b) % p = a % p - b % p;
乘法 (a * b) % p = a % p * b % p;
但是除法。。。。。。
假设:a * b % p = c, 已知 b, c, p 求 a
那么,a = c * d % p,c就是b的逆元,即1 / b
2. 逆元求法
记1 / b 为 inv (b)
求法1:
结论: ![]()
证明: 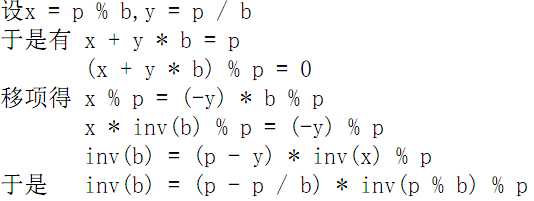
void Inv(void) {
inv[1] = 1; int p = MOD; //MOD = 1e9 + 7
for (int i=2; i<=N; ++i) {
inv[i] = (p - p / i) * inv[p%i] % p;
}
printf ("%I64d\n", 777 * 14 * inv[14] % MOD);
}
求法2:
结论: 
ll pow_mod(int a, int x, int p) {
ll ret = 1;
while (x) {
if (x & 1) ret = ret * a % p;
a = a * 1ll * a % p;
x >>= 1;
}
return ret;
}
ll Inv(int a) {
return pow_mod (a, MOD - 2, MOD);
}
标签:
原文地址:http://www.cnblogs.com/Running-Time/p/4749031.html