标签:
Problem Description
CRB has N different candies. He is going to eat K candies.
He wonders how many combinations he can select.
Can you answer his question for all K (0 ≤ K ≤ N )?
CRB is too hungry to check all of your answers one by one, so he only asks least common multiple(LCM) of all answers.
Input
There are multiple test cases. The first line of input contains an integer T , indicating the number of test cases. For each test case there is one line containing a single integer N .
1 ≤ T ≤ 300
1 ≤ N ≤ 106
Output
For each test case, output a single integer – LCM modulo 1000000007(109+7 ).
Sample Input
5
1
2
3
4
5
Sample Output
1
2
3
12
10
题目要求的是所有C(n, i) (0 <= i <= n)的最小公倍数。
这题如果直接用LCM去求会T掉,
就算离线所有n!的逆元复杂度是O(n)
然后for循环C(n, i)是O(n)
然后用LCM求最小公倍数是O(log(a)),最差情况接近O(log(10^9+7)) ~ 30
所以复杂度最差是O(30n), 300组数据,最终需要O(10^10)左右。
那个30不乘的话O(3*10^8)左右。卡了一个常数倍数量级。
题解里用了一个由Kummer定理得到的结论
Vp([C(n, 0), C(n, 1) ,.....C(n, n)]) = Vp([1, 2, ....,n+1]) - Vp(n+1)
其中Vp(k)表示k中包含质数p的次数
即max(Vp(C(n, i))) = max(Vp(i+1)) - Vp(n+1) (0 <= i <= n)
首先Kummer定理:i <= n是正整数,假设在p进制中,(n-i) + i发生了t >= 0次进位,则p^t | C(n, i)。
网上找了个证明过程
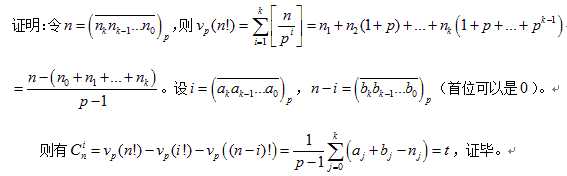
然后就是由这个证明:
当n = sum(ci*p^i), (0 <= i <= maxN)时,
max(Vp(C(n, i))) = Vp(C(n, p^maxN-1))
Case 1:
if n = p^(maxN+1)-1
Vp(C(n, p^maxN-1)) = 0
Case 2:
else
Vp(C(n, p^maxN-1)) = maxN-min(i | ci != p-1)
第一种:对于 n = p^(maxN+1)-1的情况,
显然n-i + i不管怎么加都不可能进位因为某一位最多是(p-1) + (p-1)不可能在进位的情况下还能得到p-1,既然低位没有进位,高位同理不可能得到p-1。
所以Vp(C(n, p^maxN-1)) = 0
第二种:对于 n != p^(maxN+1)-1的情况,
任意Ci必然小于等于p-1,
自然对于最低位Ci = p-1的情况,肯定是不进位得到的结果
如果最低位不进位,次低位Ci = p-1的情况,肯定也不是进位得到的。
所以对于低位都是p-1的情况都不可能进位,直到低位Ci != p-1,
此时可以开始进位,
若要让其100%进位,自然取p-1为其中一个加数,与另一个加数进位得到Ci。
然后由于从此开始每次进位,
如果遇到Ci = p-1,那么由于前一次是进位的,也就是说这次的结果是a+b+1得到的结果,此处如果a取p-1,那么就算进位,也能得到p-1,所以,此后对于任意Ci <= p-1,都可以由进位得到。
n = (CmaxN)(CmaxN-1)......(C2)(C1)(C0)
p^maxN-1 = ( p-1 ).......(p-1)(p-1)(p-1)
所以Vp(C(n, p^maxN-1)) = maxN-min(i | ci != p-1)
于是刚刚证明了这个等式左边max(Vp(C(n, i))) = max(Vp(i+1)) - Vp(n+1) (0 <= i <= n)的结论,然后证明等式右边也有相同的结论,便证明了这个等式。
首先对于max(Vp(i+1)),
假设k时取到最大值t,那么首先k的最小值为p^t,
由于p^t <= n+1,
如果n+1在p进制下的长度比n的大,那么必然n = p^(maxN+1)-1,n+1 = p^(maxN+1)。
那么右侧等于(maxN+1) - (maxN+1) = 0。
其余情况那么t自然是maxN(maxN是p进制下n+1的最大长度)
接下来就是证明Vp(n+1) = min(i | ci != p-1)了
首先对于n在p进制下最低位不是p-1的情况,那么自然n+1最低位不可能进位,不可能为0,自然Vp(n+1) = 0,右侧也为0了。
对于最低位是p-1的情况,那么n+1最低位进位得0,至少p能整除n+1了,
然后如果后面依旧是p-1那么依旧进位得0,那么知道不是p-1的那一位自然不进位了。
于是Vp(n+1)等于n低位第一个不等于p-1的,自然等于等式右侧了。
于是证毕。
max(Vp(C(n, i))) = max(Vp(i+1)) - Vp(n+1) (0 <= i <= n)
有了这个式子,就证明了[C(n, 0), C(n, 1) ,.....C(n, n)] = [1, 2, ....,n+1]/(n+1)
等式两侧的质因子指数相等,自然等式就相等了。
然后最终结果是所有p^maxN/p^k的乘积(其中maxN是p在n+1内的最高次数,k是p能整除n+1的最高次数)。
也就是所有p^maxN的乘积除以p^k的乘积,分子等于[1, 2, 3,....n+1],分母等于n+1。
这个结果和题解的结论是一致的。
证明过程有点搓。。。。
如果顺序找到k和maxN的话,复杂度是O(num*log(p)),其中num是素数个数,p是素数。
如果二分查找的话,是O(num*log(logp))
代码:O(num*log(p))
#include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <set> #include <map> #include <queue> #include <string> #include <algorithm> #define LL long long using namespace std; const LL MOD = 1e9+7; const int maxN = 1e6+5; bool isprim[maxN]; int n, prim[maxN], top; //埃氏筛法求素数 void isPrim() { memset(isprim, true, sizeof(isprim)); isprim[0] = isprim[1] = false;//初始化 for (LL i = 2; i < maxN; ++i)//筛法 { if (isprim[i]) { for (LL j = i*i; j < maxN; j += i)//上界太大可能会爆int { isprim[j] = false; } } } } void init() { isPrim(); top = 0; for (int i = 2; i < maxN; ++i) if (isprim[i]) prim[top++] = i; } void work() { LL ans = 1; for (int i = 0; i < top && prim[i] <= n+1; ++i) { for (LL v = prim[i]; v <= n+1; v *= prim[i]) { if ((n+1)%v) ans = (ans*prim[i])%MOD; } } printf("%I64d\n", ans); } int main() { //freopen("test.in", "r", stdin); init(); int T; scanf("%d", &T); for (int times = 0; times < T; ++times) { scanf("%d", &n); work(); } return 0; }
ACM学习历程—HDU5407 CRB and Candies(数论)
标签:
原文地址:http://www.cnblogs.com/andyqsmart/p/4756707.html