标签：

树与树的表示

人类的社会家谱，社会组成结构，图书信息管理。硬盘

静态查找：集合中记录是固定的。没有插入和删除，只有查找。

动态查找：集合中记录是动态变化的。除查找，还可能发生插入和删除

静态查找

就是放在数组里面，当然放链表里面也可以。方法1：顺序查找。

程序设计里面会用到一种技巧，叫做哨兵，建立一个数组，不在第0个位置就存储数据，而在第1个位置存储数据 。

哨兵的作用 ：写循环的时候可以少写一个条件。循环是倒过来做的。

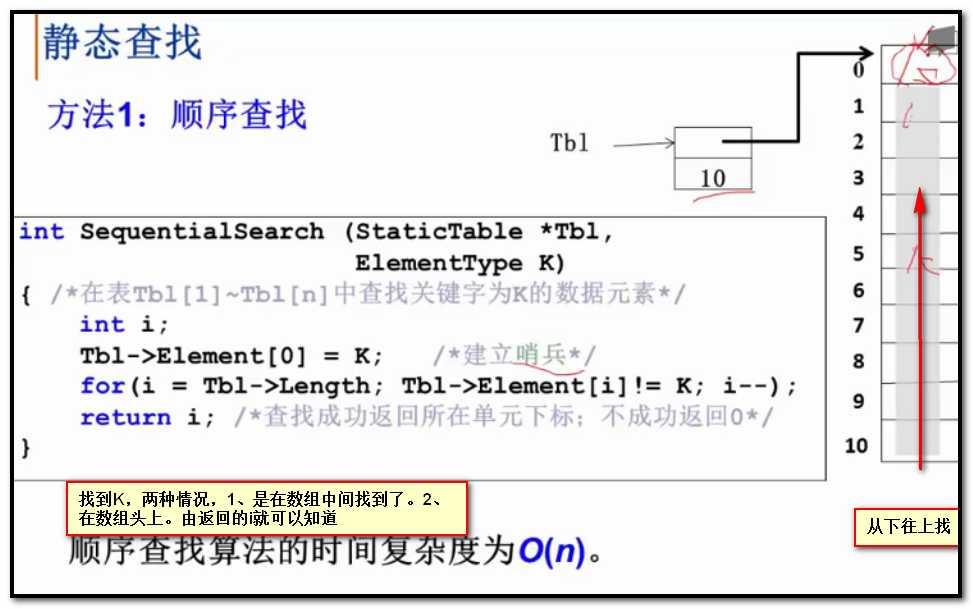
优化

方法二：二分查找 

我们把元素存到数组里面，要求的前提是必须满足有序，才能进行二分查找。 

 一直除以2 就是时间复杂度就是  log N

int BinarySearch(StaticTable *Tbl,ElementType K){　　//在表中Tbl中查找关键字为K的数据元素。
    int left, right, mid, NoFound = -1;
    left = 1;
    right = Tbl->Length;
    while (left<=right)
    {
        mid = (left + right)/2
        if (K < Tbl->ElementType[mid]) right = mid - 1;
        else if (K > Tbl->ElementType[mid]); left = mid + 1;
        else return mid;
    }
    return NotFound;
}

 二分查找的前提，就是排序。

判定树上每个结点需要的查找次数刚好为该结点所在的层数。例如：查找4需要比较三次，查找5号位置需要比较4次，

查找成功时查找次数不会超过判定树的深度  n个结点的判定树的深度为[log₂n]+1。

ASL平均查找次数 = （4*4 + 4*3 +2*2 +1*1）//11 = 3

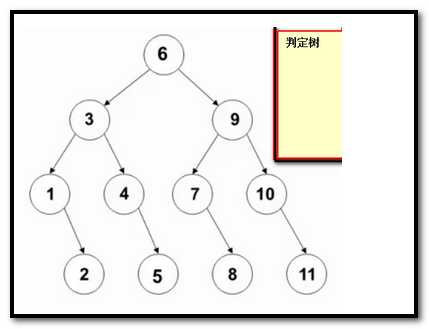
 当我们不用数组存储数据，而就把这个树存储我们需要的数据，这就是我们的查找树。查找树和二分查找效率上可以达到一样的效率。但是当在树里面插入删除结点，会比数组简单的多。所以的话，以查找树的形式可以很好的解决动态查找的问题。

 树的定义

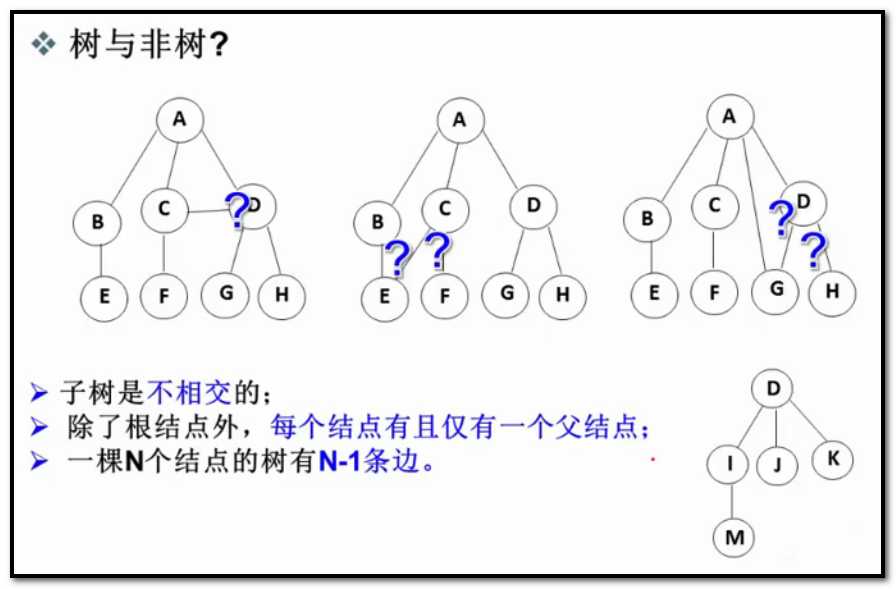
除了根结点，每个结点都有一个往上的一条边，所以一个N个结点的树有N-1条边。结点比边多一条。

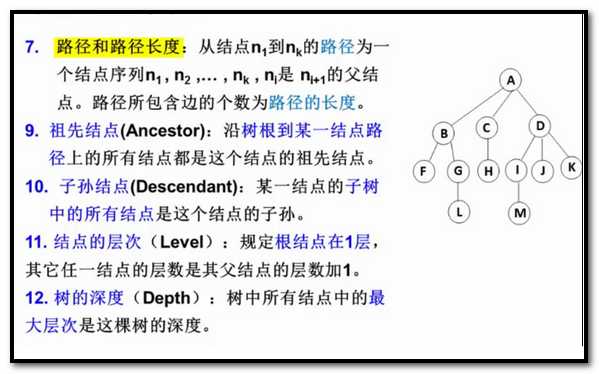
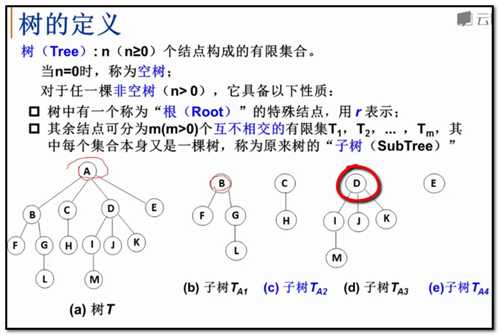
树的表示

数组实现 就算了吧。。。

 用链表来实现，就要有一个数据结构，但是呢，指针要是最大的指针。结构+链表的形式。

当用链表的时候，按照下面的设计我们要有3n个指针域，但是实际上呢，我们的边只有n-1条，2n+1都是空的，所以呢也不用链表，用什么？下面

儿子-兄弟表示法

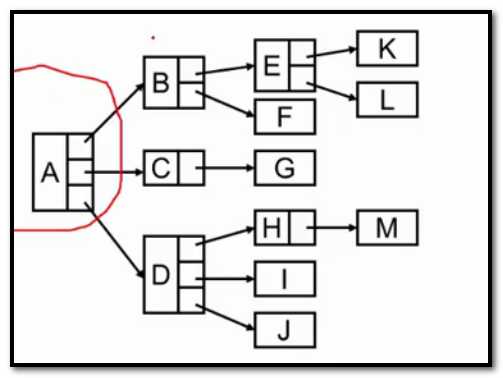
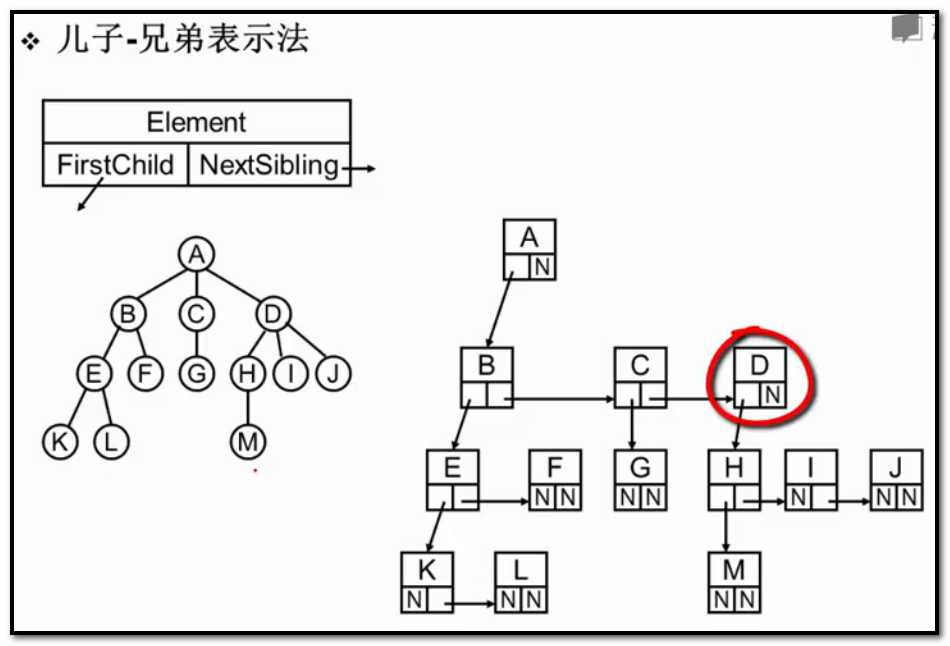
这样的表示方法，n个结点有2n个指针域，n-1个利用了，n+1个浪费了。浪费不大。把一般的树，

例：在用“儿子-兄弟”法表示的树中，如果从根结点开始访问其“次子”的“次子”，所经过的结点数与从根结点开始访问其“长子”的“长子”的“长子”的“长子”

旋转45度，这样的树呢，我们叫做二叉树。

数据结构-树-树与树的表示

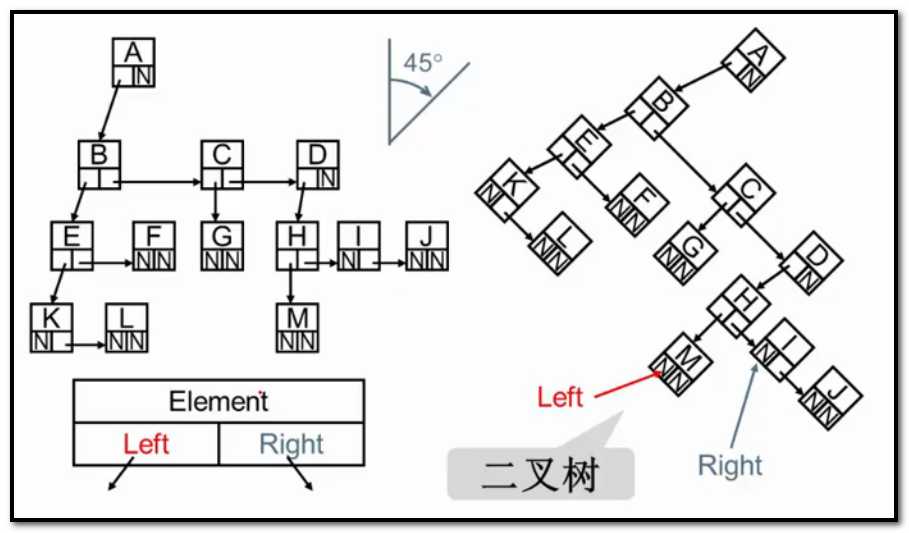
标签：

原文地址：http://www.cnblogs.com/zrui513/p/4756887.html