标签:
主要是以二叉树的链式存储来讲。
链表存储的结构:(下面会用到)
typedef struct TreeNode *BinTree; typedef BinTree Position; struct TreeNode { ElementType Data; BinTree Left; BinTree Right; }
访问顺序是根节点,左子树,右子树。这样的过程实际上就是一种递归。用递归实现
void PreOrderTraversal(BinTree BT){ if (BT){ printf("%d", BT->Data); PreOrderTraversal(BT->Left); PreOrderTraversal(BT->Right); } }
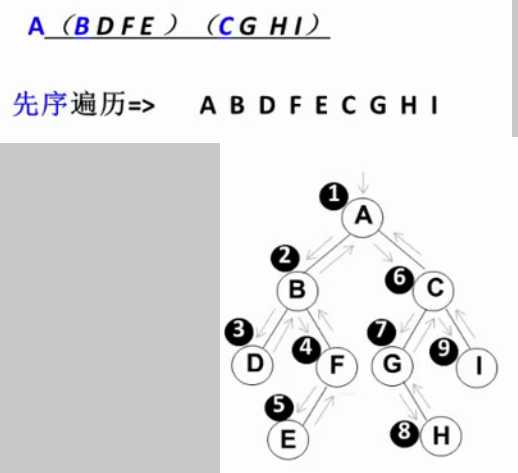
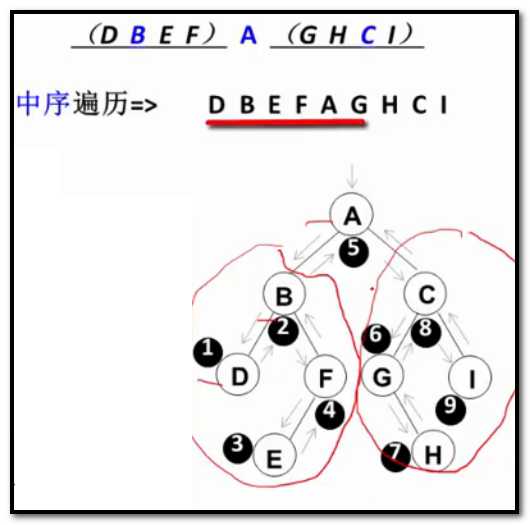
访问顺序是根节点,左子树,右子树。这样的过程实际上就是一种递归。用递归实现
void InOrderTraversal(BinTree BT){ if (BT){ InOrderTraversal(BT->Left); printf("%d", BT->Data); InOrderTraversal(BT->Right); } }
void PostOrderTraversal(BinTree BT){ if (BT){ PostOrderTraversal(BT->Left); PostOrderTraversal(BT->Right); printf("%d", BT->Data); } }
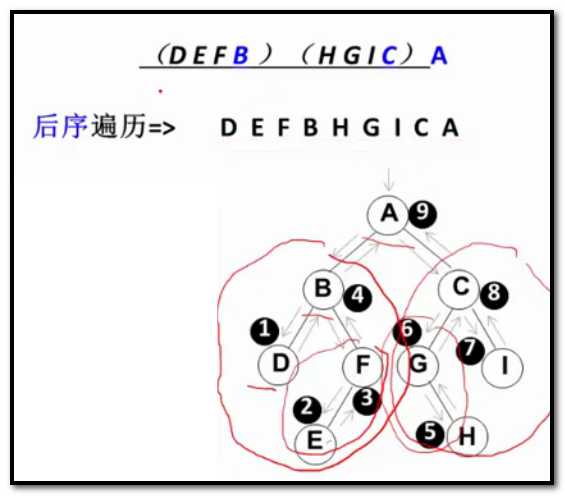
不管是前中后,走的路径都是一样的,只是访问各结点的时机不同。
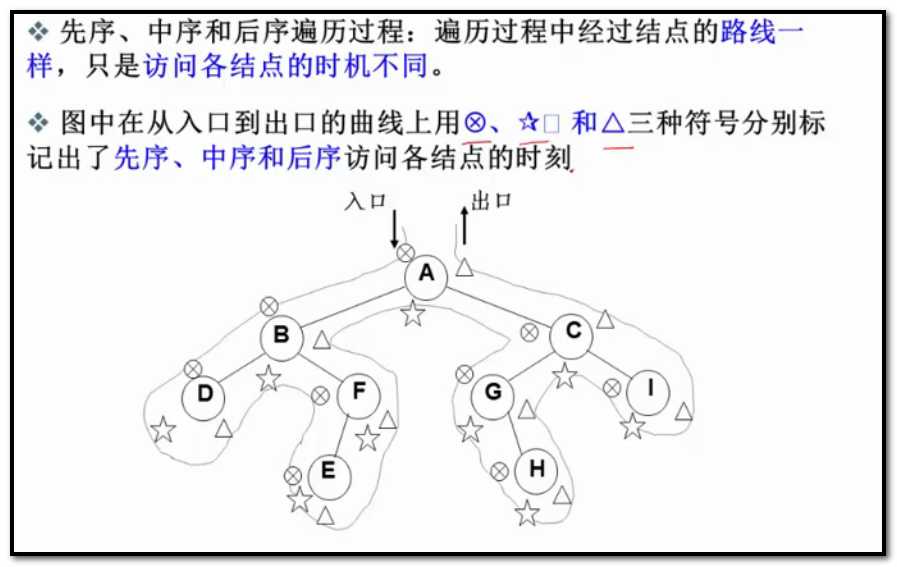
每个结点都会有三次碰到的机会,第一次碰到就输出就是前序,第二次碰到就是中序,第三次就是后序。前中后说的是根节点的遍历的次序,这三种方法都是递归的原理,递归的实现是用堆栈的,然而用堆栈也可以把递归变成非递归。×和★和?的相对顺序是不变的。
非递归算法的实现思路:堆栈
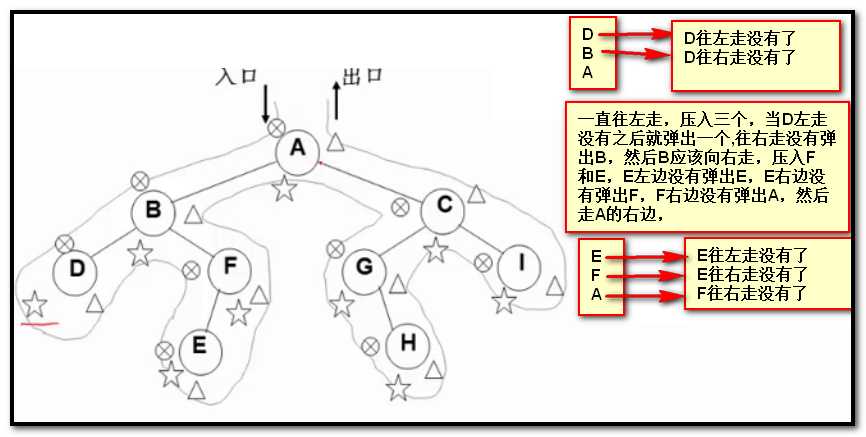
void InOrderTraversal(BinTree BT){ BinTree T = BT; //临时变量 Stack S = CreatStack(MAXSIZE); while (T|| !IsEmpty(S)) //这里判断树不空,或者堆栈不空 { while (T){ //一直想左并压入栈中 Push(S, T); // 第一次碰见这个结点,如果在这里printf, T = T->Next; } if (!IsEmpty(){ T = Pop(S); //第二次碰见这个结点的时候printf就是 printf("%5d", T->Data); T = T->Right; //进行这步是因为,他一直往左走,上面的退出循环,表示已经验证他没有左结点, //把他的右子节点赋值给T,下一下循环的时候会判断的,如果没有右结点上面的push的循环直接跳过,再出栈一个元素。 } } }
void ProOrderTraversal(BinTree BT){ BinTree T = BT; //临时变量 Stack S = CreatStack(MAXSIZE); while (T|| !IsEmpty(S)) //这里判断树不空,或者堆栈不空 { while (T){ //一直想左并压入栈中 printf("%5d", T->Data); Push(S, T); // 第一次碰见这个结点,如果在这里printf, T = T->Next; } if (!IsEmpty(){ T = Pop(S); //第二次碰见这个结点的时候printf就是 T = T->Right; //进行这步是因为,他一直往左走,上面的退出循环,表示已经验证他没有左结点, //把他的右子节点赋值给T,下一下循环的时候会判断的,如果没有右结点上面的push的循环直接跳过,再出栈一个元素。 } } }
自己解决~~~
二叉树遍历的核心问题:二维结构的线性化
层序遍历的原理是用队列保存的。
遍历就要产生结点一个序列,是一维的,线性结构,而二叉树是二维的,所以二叉树遍历的实质就是怎么将一个二维结构变成一维结构。
so 需要一个存储结构保存暂时不访问的结点,怎么记录,有两种方法:堆栈、队列,我们提到前序中序后序都可以用堆栈来实现,实际上,我们也可以用队列来实现,
队列实现:遍历从根节点开始,首先将根节点入队,然后开始执行循环:结点出队、访问该节点,其左右儿子入队
void LevelOrderTraversal(BinTree *BT) { BinTree T; Queue Q; if (!BT) return; Q = CreatQueue(MAXSIZE); /* 生成一个队列 */ AddQ(Q, BT); /* 根节点入队 */ while (!IsEmpty(Q)) { /* 队列不为空,弹出一个元素 */ T = DeleteQ(Q); if(T->Left) AddQ(Q, T->Left); if (T->Right) AddQ(Q, T->Right); /* 右子树不为空入队 */ } }
把前序遍历的程序改一改就OK
void PreOrderTraversal(BinTree BT){ if (BT){ if (!BT->Left && !BT->Right) // 如果左右儿子都不存在 printf("%d", BT->Data); PreOrderTraversal(BT->Left); PreOrderTraversal(BT->Right); } }
把前序或者中序后序遍历的程序改一改就OK 我们用后序
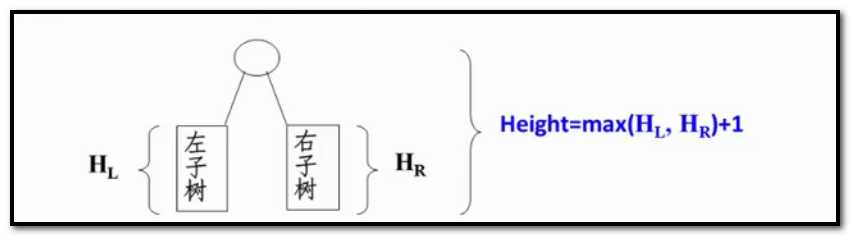
int PostOrderTraversal(BinTree BT){ int HL, HR, MaxH; if (BT){ HL = PostOrderTraversal(BT->Left); /*求左子树的深度*/ HR = PostOrderTraversal(BT->Right); /*求左子树的深度*/ MaxH = (HL > HR) ? HL : HR; /*求左右子树的深度*/ return (MaxH + 1); /*返回树的深度*/ } else return 0; /*空树的深度为0*/ }
表达式:叶结点是运算数,非叶结点是运算符号。
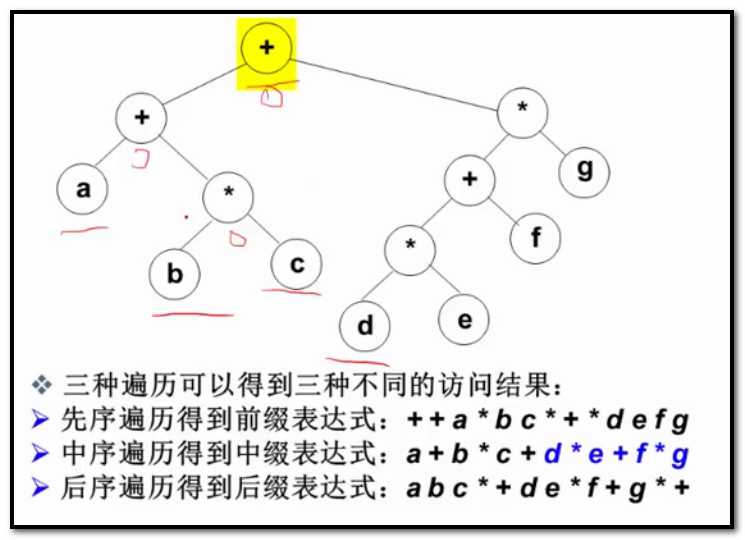
这里是什么?
前序和中序,后序和中序都可以确定一个二叉树。但是告诉我前序后序,不能确定唯一的二叉树,必须要有中序的参加。例如:
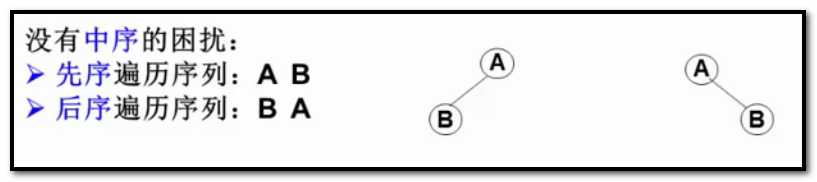
下面有前序和中序的例子及思路
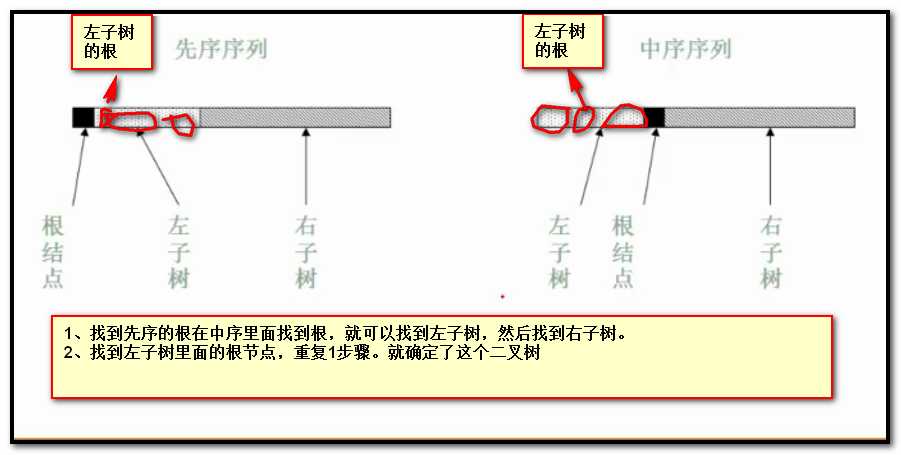
已知有棵5个结点的二叉树,其前序遍历序列是a????,中序遍历序列是a????,可以断定:A.该树根结点是a,且没有左子树
标签:
原文地址:http://www.cnblogs.com/zrui513/p/4757803.html