标签:
好吧,nginx是个幌子。主要介绍对红黑树的一些理论知识,nginx的主要源码附在后面。这篇文章并不会面面俱到,我的水平也没到那个高度。
红黑树的特性:
1.红黑树是一棵二叉搜索树。
2.树上的每个结点或为红,或为黑。
3.如果一个结点为红色,那么它的左右子结点一定为黑色。
4.从根结点到每个叶子结点路径中经过的黑色结点数是相同的。
5.根结点必须是黑色。
理解这些特性是很重要的。正是因为有这些特性,才保证了红黑树的高效。(至于为什么,我学的还不精,不乱讲了。)。
红黑树的插入和删除结点动作本质上还是按照二叉搜索树的规则来进行的。不过在基本操作完成后,如果违反了红黑树的某个特性,这时才需要做一些旋转操作进行红黑结点的平衡。所以说,红黑树相当一部分的插入和删除动作就是基本的二叉搜索树的插入和删除。本文只列举那些需要旋转处理的情况。
红黑树的插入操作:
约定如下:当前操作结点为X,X的父节点为P,P的父节点PP,P的兄弟结点为S。
根据规则4,新插入的结点(X)必须是red。如果X的父节点(P)也是red。那么违反了规则3,必须通过旋转操作以满足特性。分为三种情况。
I1:
X为red,P为red,S为black。可以推导出PP也为black。
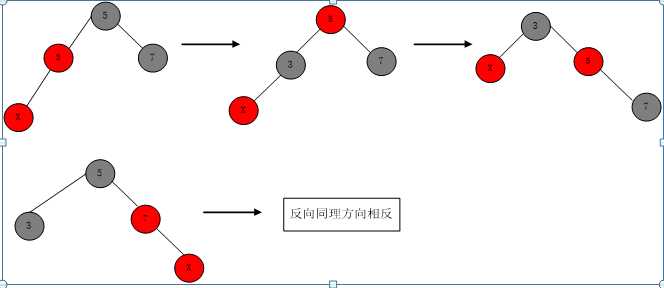
分为三步:将P置black,将PP置红,PP右旋转。(反向同理)。
I2:
X为red,P为red,S为black。可以推导出PP也为black。
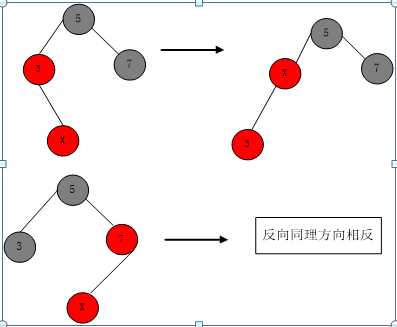
直接将P左旋转,此时变成了I1。按照I1步骤进行平衡(反向同理,方向相反)。
I3:
X为red,P为red,S为red。可以推导出PP为black。
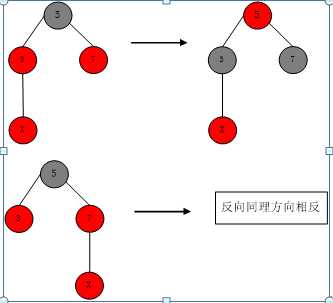
这种情况将P和S置black,将PP置red。这种情况比较特殊,如果PP的父节点PPP也为red呢?那么以P结点为新的X向上递归。直到PPP为黑。如果递归到root结点,那么直接设置root为black即可。(相当于每个路径中的black结点数同时+1)。
至此,红黑树的插入操作理论就全部讲完了,我说清了吗?
红黑树的删除操作:
红黑树的删除操作第一步也遵循二叉搜索树的规律。
我们假设要删除的结点为Y。分为三种情况:
至此结点的删除已经完成,第二步就是平衡红黑结点,是树满足红黑树的性质。
约定如下:当前操作结点为X,X的父节点为P,X的兄弟结点为S(注意这里是X的兄弟)。S的子结点为Sl Sr。
D1:
X为black,S为red。则Sl Sr必为black。
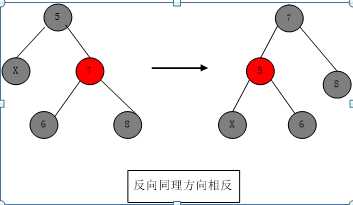
变换后并没有使树满足红黑树的性质,而是把它转换为了另一种情况。(D2 D3 D4)。
D2:
X为black,S为black。则Sl Sr为black。
因为删除X,所以X分支比S分支少一个black结点。将S置red后,整个子树左右分支black结点平衡(比其他分支少一个)。所以将P设置为新的X。(这里理解比较容易,不画图了)。
D3:
X为black,S为black。则Sl 为red Sr位black。
S置red Sl置black。 S右旋转。转化成D4。
D4:
X为black,S为black。则Sl 为black Sr位red。
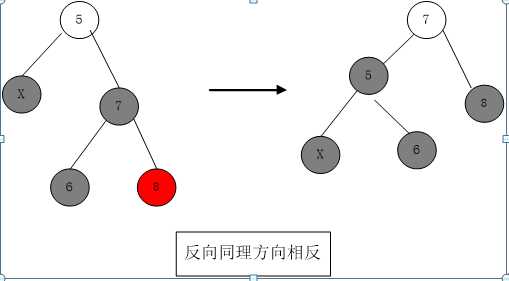
将S设置为P的颜色,P置black。置Sr为black。左旋转P。这样左子树缺失的black结点补回来了。删除完成。
可见当删除结点有左右子树时,只有D4,才能真正完成平衡。D1 D2 D3都是向D4转化。
说到后面自己都懵圈了,感觉要出丑。写都写了,还是发出来吧。
为什么我上面的理论说的这么简单粗暴呢?nginx就是这么写的呀。
插入代码:
void ngx_rbtree_insert(ngx_rbtree_t *tree, ngx_rbtree_node_t *node) { ngx_rbtree_node_t **root, *temp, *sentinel; /* a binary tree insert */ root = (ngx_rbtree_node_t **) &tree->root; sentinel = tree->sentinel; //sentinel为哨兵,我觉得就是NULL if (*root == sentinel) { node->parent = NULL; node->left = sentinel; node->right = sentinel; ngx_rbt_black(node); *root = node; return; } tree->insert(*root, node, sentinel); //按照二叉搜索树插入结点 /* re-balance tree */ while (node != *root && ngx_rbt_is_red(node->parent)) { //平衡红黑结点 if (node->parent == node->parent->parent->left) { temp = node->parent->parent->right; if (ngx_rbt_is_red(temp)) { //I3 ngx_rbt_black(node->parent); ngx_rbt_black(temp); ngx_rbt_red(node->parent->parent); node = node->parent->parent; } else { if (node == node->parent->right) { //I2 node = node->parent; ngx_rbtree_left_rotate(root, sentinel, node); } ngx_rbt_black(node->parent); //I1 ngx_rbt_red(node->parent->parent); ngx_rbtree_right_rotate(root, sentinel, node->parent->parent); } } else { //反向同理,方向相反。 temp = node->parent->parent->left; if (ngx_rbt_is_red(temp)) { ngx_rbt_black(node->parent); ngx_rbt_black(temp); ngx_rbt_red(node->parent->parent); node = node->parent->parent; } else { if (node == node->parent->left) { node = node->parent; ngx_rbtree_right_rotate(root, sentinel, node); } ngx_rbt_black(node->parent); ngx_rbt_red(node->parent->parent); ngx_rbtree_left_rotate(root, sentinel, node->parent->parent); } } } ngx_rbt_black(*root); //无脑设置,任何情况都对。 }
删除代码:
void ngx_rbtree_delete(ngx_rbtree_t *tree, ngx_rbtree_node_t *node) { ngx_uint_t red; ngx_rbtree_node_t **root, *sentinel, *subst, *temp, *w; /* a binary tree delete */ root = (ngx_rbtree_node_t **) &tree->root; sentinel = tree->sentinel; //哨兵(NULL) if (node->left == sentinel) {//情况1 2 删除结点Y为单支结点或者叶子结点 temp = node->right; subst = node; } else if (node->right == sentinel) {//情况1 2 删除结点Y为单支结点或者叶子结点 temp = node->left; subst = node; } else { //情况1 情况3 删除结点Y为双支结点 subst = ngx_rbtree_min(node->right, sentinel); if (subst->left != sentinel) { temp = subst->left; } else { temp = subst->right; } } if (subst == *root) { *root = temp; ngx_rbt_black(temp); /* DEBUG stuff */ node->left = NULL; node->right = NULL; node->parent = NULL; node->key = 0; return; } red = ngx_rbt_is_red(subst); //记录Y的颜色 if (subst == subst->parent->left) { //这里是按照二叉搜索树的性质,删除结点后重新生成二叉搜索树。 subst->parent->left = temp; } else { subst->parent->right = temp; } if (subst == node) { temp->parent = subst->parent; } else { if (subst->parent == node) { temp->parent = subst; } else { temp->parent = subst->parent; } subst->left = node->left; subst->right = node->right; subst->parent = node->parent; ngx_rbt_copy_color(subst, node); if (node == *root) { *root = subst; } else { if (node == node->parent->left) { node->parent->left = subst; } else { node->parent->right = subst; } } if (subst->left != sentinel) { subst->left->parent = subst; } if (subst->right != sentinel) { subst->right->parent = subst; } } /* DEBUG stuff */ node->left = NULL; node->right = NULL; node->parent = NULL; node->key = 0; if (red) { //删除结点Y为red 直接退出 return; } /* a delete fixup */ while (temp != *root && ngx_rbt_is_black(temp)) { //temp就是上文中的X。开始平衡红黑结点。直到X为红色,或者到达root if (temp == temp->parent->left) { w = temp->parent->right; if (ngx_rbt_is_red(w)) { //D1 ngx_rbt_black(w); ngx_rbt_red(temp->parent); ngx_rbtree_left_rotate(root, sentinel, temp->parent); w = temp->parent->right; } if (ngx_rbt_is_black(w->left) && ngx_rbt_is_black(w->right)) {//D2 ngx_rbt_red(w); temp = temp->parent; } else { if (ngx_rbt_is_black(w->right)) { //D3 ngx_rbt_black(w->left); ngx_rbt_red(w); ngx_rbtree_right_rotate(root, sentinel, w); w = temp->parent->right; } ngx_rbt_copy_color(w, temp->parent); //D4 ngx_rbt_black(temp->parent); ngx_rbt_black(w->right); ngx_rbtree_left_rotate(root, sentinel, temp->parent); temp = *root; } } else { //反向同理,方向相反。 w = temp->parent->left; if (ngx_rbt_is_red(w)) { ngx_rbt_black(w); ngx_rbt_red(temp->parent); ngx_rbtree_right_rotate(root, sentinel, temp->parent); w = temp->parent->left; } if (ngx_rbt_is_black(w->left) && ngx_rbt_is_black(w->right)) { ngx_rbt_red(w); temp = temp->parent; } else { if (ngx_rbt_is_black(w->left)) { ngx_rbt_black(w->right); ngx_rbt_red(w); ngx_rbtree_left_rotate(root, sentinel, w); w = temp->parent->left; } ngx_rbt_copy_color(w, temp->parent); ngx_rbt_black(temp->parent); ngx_rbt_black(w->left); ngx_rbtree_right_rotate(root, sentinel, temp->parent); temp = *root; } } } ngx_rbt_black(temp); //置black }
我这写的真是shit啊。研究nginx源码的凑合着看吧。红黑树研究透了卷土重写。轻点吐槽。
标签:
原文地址:http://www.cnblogs.com/acool/p/4758397.html