标签:
以下纯属个人理解;如有什么不对的请多联系指教。
有参考(http://wenku.baidu.com/link?url=R47d3QatLS8UsDWNIlSEOyvgVNFiLr8AZnhiPJ7_ur_sH4xoeZUfjFhL4zjE0P6bpDtqx3L9_2jlrNMJGJJLpgE-5ycrRqbaJ1ZEZckhFum)
4.为什么要进行等价类的划分?等价类划分应该遵循哪些原则?
答案:使用等价类测试方法可以大大减少测试用例的数目,从而提高测试效率。 特点:完备性--划分出的各个等价类(子集)并不是输入/输出的全集,即程序的定义域/值域;无冗余性--各个等价类是互不相交的一组子集;等价性--划分的各个子集是由等价关系决定的,即各个输入数据对于揭露程序中的错误都是等效的。
原则:
1)在输入条件规定了取值范围的情况下,可确立一个有效等价类和两个无效等价类;
2)在输入条件规定了输入值的个数的情况下,可确立一个有效等价类和两个无效等价类;
3)在输入条件规定了输入值的集合或者规定了"必须如何"的条件的情况下,可确立一个有效等价类和多个无效等价类;
4)在输入条件是一个布尔量的情况下,可确定一个有效等价类和一个无效等价类;
5)在规定了输入数据的一组值(假定n个),并且程序要对每一个输入值分别处理的情况下,可确立n个有效等价类和一个无效等价类;
6)在规定了输入数据必须遵守的规则的情况下,可确立一个有效等价类和多个无效等价类;
5.针对以下问题:某一种8位计算机,其十六进制常数的定义是以0x或0X开头的十六进制整数,其取值范围为-7f~7f(不区分大小写字母),如0x11、0x2A、-0x3c,请采用等价类划分的方法设计测试用例。
答案:min=-7f max=7f
值value 有效等价类:-7f<=value<=7f;无效等价类:value< -7f,value > 7f;
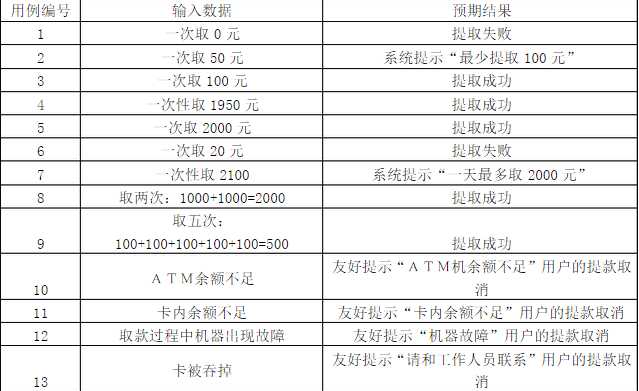
6.假定一台ATM机允许提取增量为50元,总金额从100~2000(包含2000)不等的现金,请结合等价类方法和边界值分析进行测试。
答案:min=100 max=2000
取值money有效等价类:100<=money<=2000;(money为50的倍数) 无效等价类:money<100,money>2000,money不是50的倍数。
测试用例:
7.有一个小学生成绩管理系统,要求把成绩好的同学放在前面,其中每个人都有三门课程成绩:语文,数学,英语。首先是按个人的总成绩进行排名,如果两个人的总分相等则按他们的语文成绩进行排名,如果总成绩和语文成绩都想同,则按照他们的数学成绩排名,请用等价类方法进行排名。
答案:总成绩total,语文:Chinese,数学:math,英语:English
有效类:Ta≠Tb,按总成绩total排名 Ta=Tb && Ca≠Cb,按语文成绩(Chinese)排名 Ta=Tb && Ca=Cb && Ma≠Mb按数学成绩(math)排名;
无效类:Ta=Tb && Ca=Cb && Ma=Mb。
思考题:有20个输入量,其中有3个是多缺陷,17个是单缺陷,求总测试用例数量。
答案:弱一般等价类测试:17+3=20
强一般等价类测试:17*3=51
弱健壮等价类测试:3x17+3x3x3=78
强健壮等价类测试:3x17*3x3x3=1377
附:
弱一般等价类:单缺陷假设,不讨论异常区域
强一般等价类:多缺陷假设,不考虑异常区域
弱健壮等价类:单缺陷假设,要考虑异常区域
强健壮等价类:多缺陷假设,要考虑异常区域;即一个全笛卡尔乘积
标签:
原文地址:http://www.cnblogs.com/Decmber/p/4758865.html