标签：
参考：理解SVM三层境界
原来的分类函数：
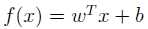
通过对偶问题求解得到：
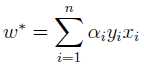
所以分类函数被转换成：
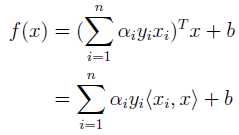
线性核函数的预测：
使用线性核函数（相当于没有使用核函数）的情况下，推导到此结束。对于新点x的预测，只需要计算它与训练数据点的内积即可，而所有的非支持向量所对应的系数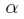
都是等于0的，因此对于新点的内积计算实际只要针对少量的支持向量。【此处表明，当模型训练好，只需要保留参数和支持向量即可】
Ps:怎么理解支持向量是少数的？
拉格朗日乘子法得到的目标函数：
????
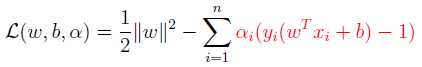
注意到如果x是支持向量的话，上式中红颜色的部分是等于0的(因为支持向量的functional margin 等于1)，而对于非支持向量来说，functional margin 会大于1 ，因此红颜色部分是大于零的，而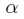
又是非负的，为了满足最大化，
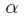必须等于0
?
引入核函数：
引入映射后的分类函数：
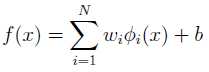
通过对偶问题求解得到：
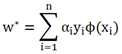
所以分类函数被转换成：
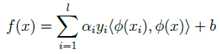
PS：核函数其实就是两个向量经过映射后的内积表达式。在核函数中只需要对映射之前的两个向量进行操作（内积、距离计算等等），得到的结果相当于映射之后的高维向量的内积结果。
带核函数的预测：
????对于新点x的预测，需要计算它与训练数据点映射后的内积（调用核函数），同样的，所有的非支持向量所对应的系数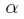
都是等于0的，因此对于新点的计算实际只要针对少量的支持向量。
????由于高斯核的特殊性，核函数中有计算两个向量的距离，所以如果数据没有规范化的话，大值数据会掩盖小值数据。
?
标签：
原文地址：http://www.cnblogs.com/xiangzhi/p/4759285.html
