标签:
描述:
There are many magic numbers whose lengths are less than 10. Given some queries, each contains a single number, if the Levenshtein distance (see below) between the number in the query and a magic number is no more than a threshold, we call the magic number is the lucky number for that query. Could you find out how many luck numbers are there for each query?
In information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences.
The term edit distance is often used to refer specifically to Levenshtein distance.
The Levenshtein distance between two strings is defined as the minimum number of edits needed to transform one string into the other, with the allowable edit operations being insertion, deletion, or substitution of a single character. It is named after Vladimir Levenshtein, who considered this distance in 1965.
For example, the Levenshtein distance between "kitten" and "sitting" is 3, since the following three edits change one into the other, and there is no way to do it with fewer than three edits:
1.kitten → sitten (substitution of ‘s‘ for ‘k‘)
2.sitten → sittin (substitution of ‘i‘ for ‘e‘)
3.sittin → sitting (insertion of ‘g‘ at the end).
There are several test cases. The first line contains a single number T shows that there are T cases. For each test case, there are 2 numbers in the first line: n (n <= 1500) m (m <= 1000) where n is the number of magic numbers and m is the number of queries.
In the next n lines, each line has a magic number. You can assume that each magic number is distinctive.
In the next m lines, each line has a query and a threshold. The length of each query is no more than 10 and the threshold is no more than 3.
For each test case, the first line is "Case #id:", where id is the case number. Then output m lines. For each line, there is a number shows the answer of the corresponding query.
代码:
这里提到了levenshtein distance,特去维基百科查阅。In information theory and computer science, the Levenshtein distance is a string metric for measuring the difference between two sequences.Levenshtein distance between two words is the minimum number of single-character edits (i.e. insertions, deletions or substitutions) required to change one word into the other.也就是从一个字符串经过增、删、改变换到另一个字符串所需要的最少操作步骤。
求levenshtein distance有已有的算法:
Mathematically, the Levenshtein distance between two strings  (of length
(of length  and
and  respectively) is given by
respectively) is given by 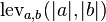 where
where
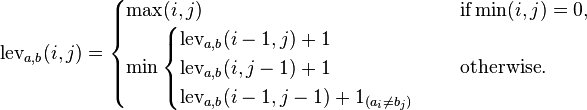
where 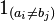 is the indicator function equal to 0 when
is the indicator function equal to 0 when  and equal to 1 otherwise.
and equal to 1 otherwise.
先描述一下算法的原理:
为了更加清晰的理解,我们用一个二维表来理解:
| b | e | a | u | t | y | ||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| b | 1 | ||||||
| a | 2 | ||||||
| t | 3 | ||||||
| y | 4 | ||||||
| u | 5 |
初始的时候,第一行与第一列初始化为0-n,代表利用insertion操作从空串依次插入,得到当前的串。
| b | e | a | u | t | y | ||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| b | 1 | 0 | |||||
| a | 2 | ||||||
| t | 3 | ||||||
| y | 4 | ||||||
| u | 5 |
dp[1][1]的值由左方、上方和左前方的值决定。从左方来,意味着从beauty的空到batyu的b,只需要一次insertion操作,操作数和为1+1;从上方来与从左方来类似,操作数为1+1;从左上方来,由于beauty的b与batyu的b相等,所以不需要进行操作,操作数为0+0。选取最小值0+0位dp值。
| b | e | a | u | t | y | ||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| b | 1 | 0 | 1 | ||||
| a | 2 | 1 | |||||
| t | 3 | ||||||
| y | 4 | ||||||
| u | 5 | |
同理,我们可以填出其他值。
根据算法的原理,可以解决这道题。这道题求的是一大堆串与给定串的编辑距离小于等于给定threshold(阈值)的个数。
#include<stdio.h> #include<string.h> #include<iostream> #include<stdlib.h> #include <math.h> using namespace std; #define N 15 #define M 1505 int MIN( int a,int b,int c ){ if( b<a ) a=b; if( c<a ) a=c; return a; } int main(){ int T,tc=1,count,magic_num,query_num,threshold,dp[N][N],cost; char magic[M][N],query[N]; scanf("%d",&T); while( tc<=T ){ scanf("%d%d",&magic_num,&query_num); for( int i=0;i<magic_num;i++ ) scanf("%s",magic[i]); for( int i=0;i<N;i++ ){ dp[0][i]=i; dp[i][0]=i; } printf("Case #%d:\n",tc); while( query_num-- ){ scanf("%s%d",&query,&threshold); count=0; for( int i=0;i<magic_num;i++ ){ for( int j=1;j<=strlen(magic[i]);j++ ){ for( int k=1;k<=strlen(query);k++ ){ if( magic[i][j-1]==query[k-1] ) cost=0; else cost=1; dp[j][k]=MIN(dp[j-1][k]+1,dp[j][k-1]+1,dp[j-1][k-1]+cost); } } if( dp[strlen(magic[i])][strlen(query)]<=threshold ) count++; } printf("%d\n",count); } tc++; } system("pause"); return 0; }
HDU4323-Magic Number(levenshtein distance-编辑距离)
标签:
原文地址:http://www.cnblogs.com/lucio-yr/p/4759975.html