标签:
这里的堆不是堆栈,排队不完全按照时间的先后顺序,有优先的级别。排队的原则有哪些?
优先队列:特殊的“队列”,取出元素的顺序是依照元素的优先权(关键字)大小,而不是元素进入队列 的先后顺序。
那么怎么实现优先队列呢?数组或者是链表?见下图

是否可以用二叉树存储结构?
二叉搜索树? 查找和删除都是树的高度log2n,可能一直删除最大值,但是删除几次之后,我们就不用查找树,搜索树。
还有别的方法吗?
那我们怎么组织二叉树呢?
最好的 方法就是用完全二叉树。堆最大的特点就是用完全二叉树,任何一个节点都比他的左右儿子结点大。
堆的两个特性
结构性:用数组表示的完全二叉树
有序性:任何一个节点都比他的左右儿子结点大。

首先,我们看一下,堆这个数据结构,我们怎么定义
typedef struct HeapStruct *MaxHeap; struct{ ElementType *Elements; //存储堆元素的数组 int Size; //堆的当前元素个数 int Capacity; //堆的最大容量 }
MaxHeap Create(int MaxSize){ MaxHeap H = malloc(sizeof(struct HeapStruct)); H->Elements = malloc((MaxSize + 1)*sizeof(ElementType)); //这里因为堆是从下标为1开始的,不是0,所以申请数组空间的时候要+1 H->Size = 0; H->Capacity = MaxSize; H->Elements[0] = MaxData; //这里用作岗哨,用作哨兵用 return H; }
思路是:先把元素放在最后一个位置,以满足完全二叉树的结构性,然后再循环满足二叉树的有序性。
void Insert(MaxHeap H, ElentType item){ int i; if (isfull(H)){ printf("最大堆已满"); return; } i = ++H->Size; for (; H->ElementType[i / 2); i /= 2) //有一种情况:当我们比到第一个元素的时候,按照循环还要向前比较,如果我们不用哨兵可以 &&i>1 H->Element[i] = H->Element[i / 2]; //这时候哨兵就有作用了,安排一个特别大的值做哨兵 H->Elements[i] = item; //就爱那个items }
插入的时间复杂性呢是T(N) = O(log2N) ,就是树的高度
最大堆删除,删除的位置是确定的,一定是根的位置、
思路是,删除第一个元素,然后让完全二叉树的最后一个元素来替它满足二叉树的结构性,再来循环满足有序性
ElementType DeleteMax(MaxHeap H){ int Parent, Child; ElementType MaxItem, temp; if (IsEmpty(H)){ printf("最大堆为空"); return; } MaxItem = H->Elements[1]; temp = H->ElementType[H->Size--];
//这个循环的作用就是找到parents的位置 for (Parent = 1; Parent * 2 <= H->Size; Parent = Child) { Child = Parent * 2; if (Child != H->Size && (H->Elments[Child] < H->ElmentType[Child + 1])) //判断有没有右儿子,并且右儿子比左儿子大,则用右儿子 Child++; if (temp >= H->Elments[Child]) break; else H->Elements[Parent] = H->Elements[Child]; } H->Elements[Parent] = temp; return MaxItem; }
时间复杂性还等于树的高度T(N) = log2n
堆的一个应用:堆排序
建立最大堆:将已经存在的N个元素按最大堆的要求存放在一个一维数组中。
方法1、通过插入操作,将N个元素一个个相继插入到一个初始为空的堆中去。其时间代价为O(NlogN).
优化之后
方法2、在线性时间复杂度下建立最大堆。
(1)将N个元素入,按输入顺序存先满足完全二叉树的结构特性。
(2)调整各节点位置,以满足最大堆的有序特性。
一点一点的调成堆
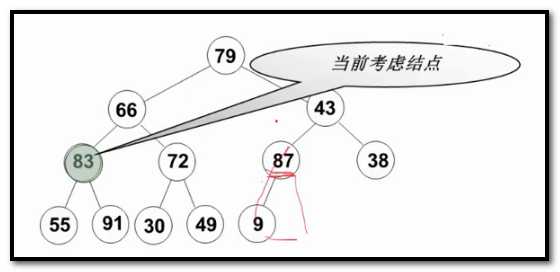
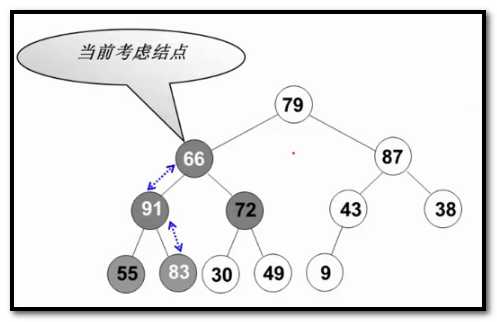
标签:
原文地址:http://www.cnblogs.com/zrui513/p/4760577.html