标签：

什么是哈夫曼树？

 编码这个问题，二进制的形式，等长码。出现频率高的 不登场编码，效率能提高。

将百分制的考试成绩转换成五分制的成绩。

判定树

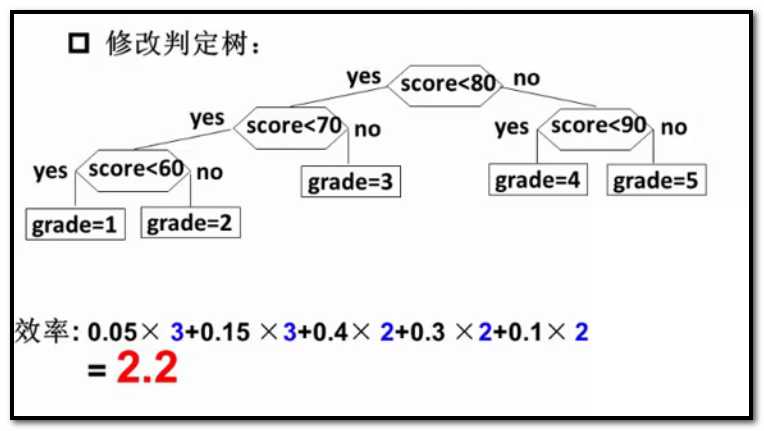
 同一件事情，我们用了不通的判定树，就得出了不同的效率

so........如何根据结点不通的查找频率构造更有效地搜索树？这就是哈夫曼舒要解决的问题。

哈夫曼树的定义：

　　带权路径长度（WPL）：设二叉树有n个叶子节点，每个叶子节点带有权重w_k，从根节点到叶子节点的长度为lk，则每个叶子节点的带权路径长度之和就是

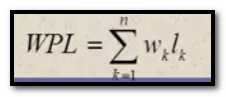
哈夫曼树又叫最优二叉树。 哈夫曼树就是让WPL值最小。

 哈夫曼树的构造

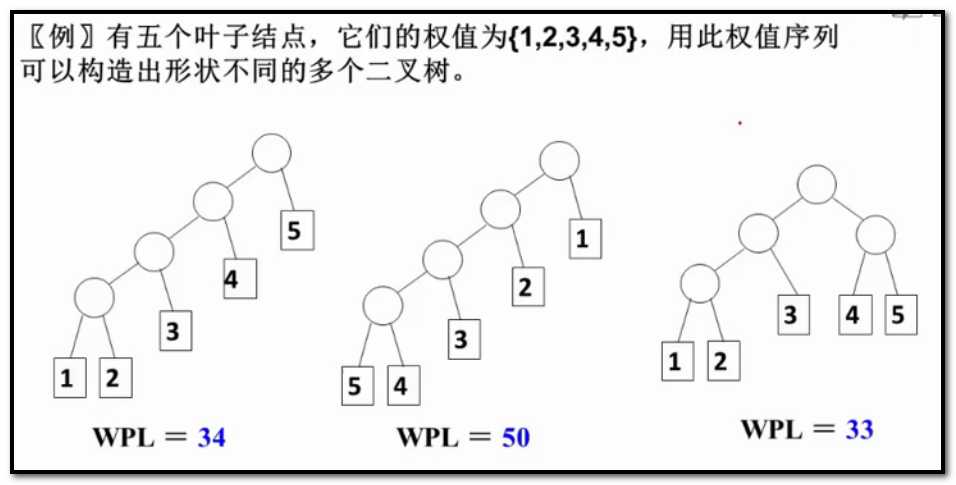
 哈夫曼树的思路 ：就是把权值从小到大进行排序，每次把权值最小的两课二叉树合并，形成一个新的二叉树，

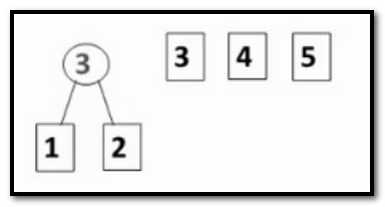
 然后把权值最小的两个结点再并在一起，也就是把3 3 4 5 并在一起。第一个3 就是1  和 2 的权值的和。最后形成了下图

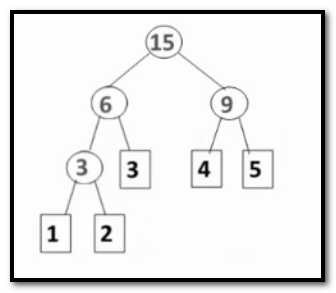
哈夫曼树的算法：

思路，如何找到最小的两个元素呢？实际上就是堆的问题，建立一个最小堆，找到里面最小的两个元素。

HuffmanTree Huffman(MinHeap H){
    int i; HuffmanTree T;
    BuildMinHeap(H); 
    for ( i = 0; i < H->Size; i++)
    {
        T = malloc(sizeof(struct TreeNode));  //建立新结点
        T->Left = deleteMin(H);                //删除一个结点，作为最小堆的左子节点。
        T->Right = deleteMin(H);            //删除一个结点，作为最小堆的右子节点。
        T->Weight = T->Left->Weight + T->Right->Weight;
        Insert(H, T);        //将新T插入最小堆
    }
    T = deleteMin(H);
    return T;
}

最大的时间复杂性是nlog₂n

 哈夫曼树的几个特点：

1. 没有度为1 的结点。因为哈夫曼树本来就是找到两个最小的来合并的。
2. n个叶子节点的哈夫曼树共有2n-1个结点
   1. n0 有n个。
   2. n1 哈夫曼树是没有度为1 的结点的。
   3. n2  n0 = n2 + 1;
3. 哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树。
4. 对同一组权值｛w1,w2,w3｝，是否存在不同构的两颗哈夫曼树呢？  是的，可能存在

 哈夫曼编码

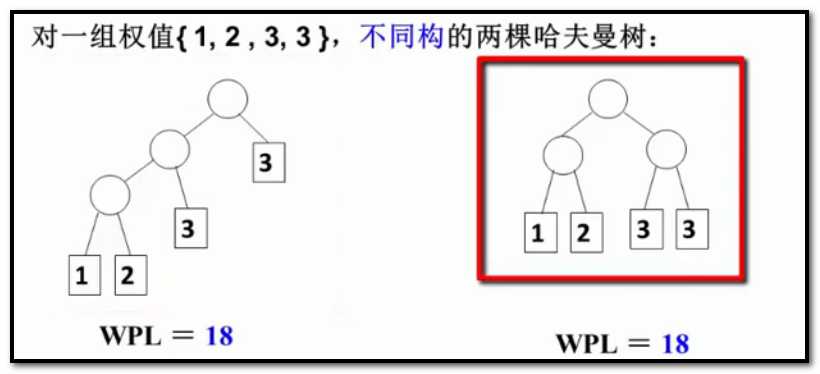
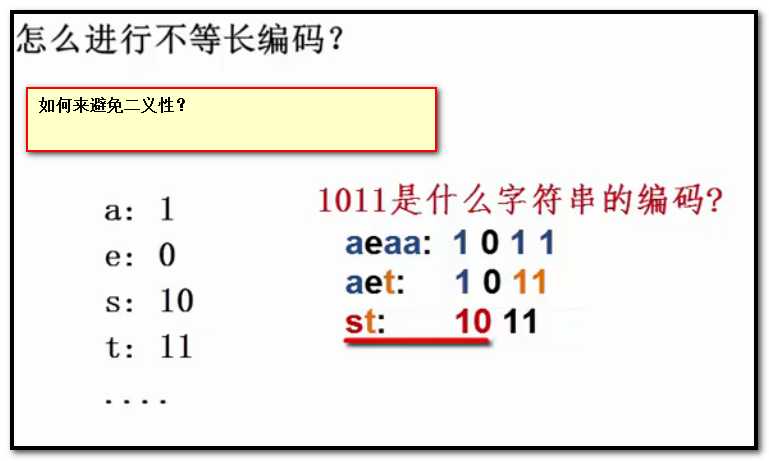
如何来避免二义性呢？

前缀码：人和字符的编码都不是另一字符编码的前缀

• 可以无二义的编码。

用二叉树来用于编码

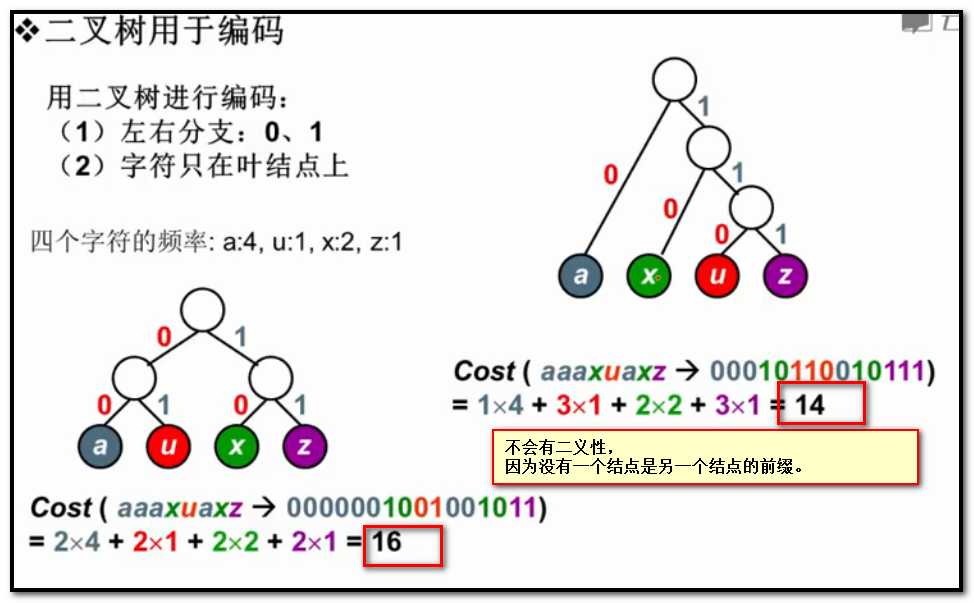
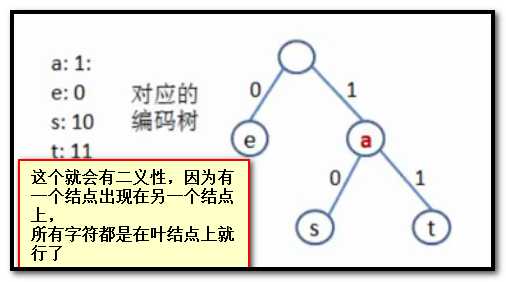
怎么用哈夫曼树来构造这样的非登场编码

数据结构--树（下）--哈夫曼树与哈夫曼编码

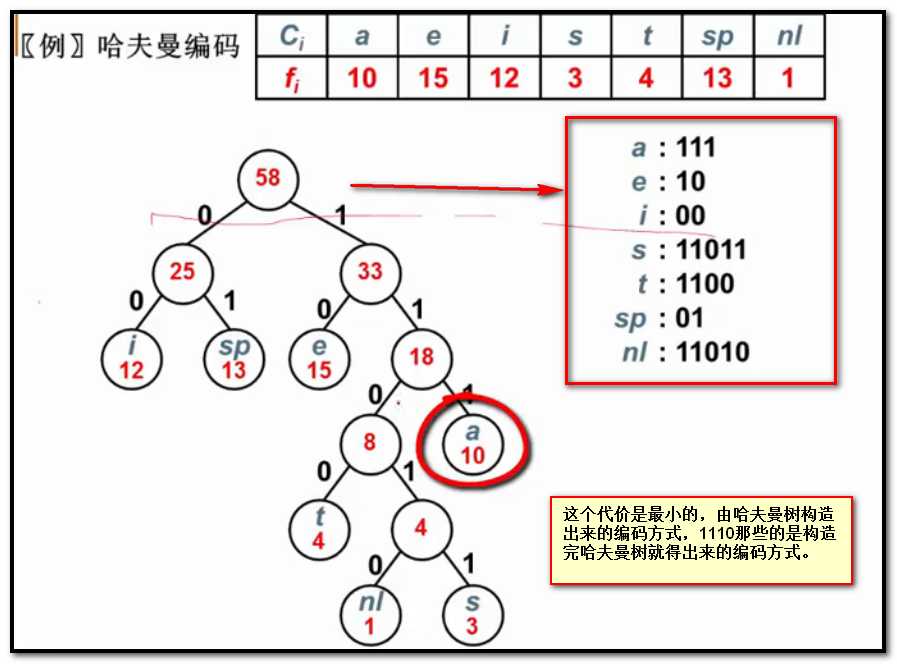
标签：

原文地址：http://www.cnblogs.com/zrui513/p/4760582.html