标签:
今天把kmp的原理回顾了一下,于是做一下总结
感谢该作者给出详尽的解释http://www.cnblogs.com/yjiyjige/p/3263858.html
简单阐明一下原理
KMP在寻找字符串匹配的过程中 保持主串的指针不动 每次匹配不成功 只对模式串进行处理
“
接下来我们自己来发现j的移动规律:
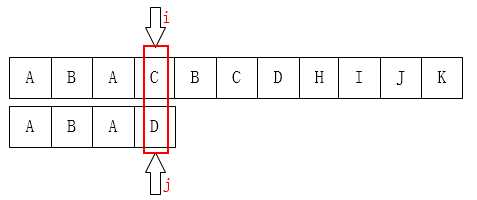
如图:C和D不匹配了,我们要把j移动到哪?显然是第1位。为什么?因为前面有一个A相同啊:
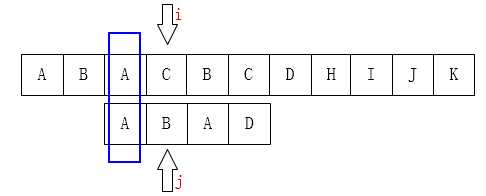
如下图也是一样的情况:
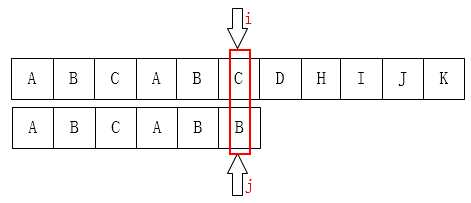
可以把j指针移动到第2位,因为前面有两个字母是一样的:
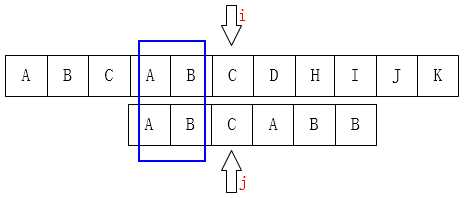
至此我们可以大概看出一点端倪,当匹配失败时,j要移动的下一个位置k。存在着这样的性质:最前面的k个字符和j之前的最后k个字符是一样的。
如果用数学公式来表示是这样的
P[0 ~ k-1] == P[j-k ~ j-1]
这个相当重要,如果觉得不好记的话,可以通过下图来理解:
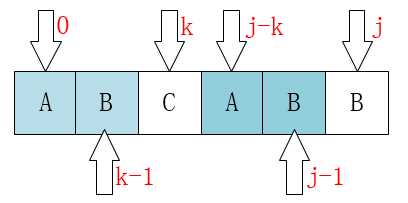
弄明白了这个就应该可能明白为什么可以直接将j移动到k位置了。
因为:
当T[i] != P[j]时
有T[i-j ~ i-1] == P[0 ~ j-1]
由P[0 ~ k-1] == P[j-k ~ j-1]
必然:T[i-k ~ i-1] == P[0 ~ k-1]
公式很无聊,能看明白就行了,不需要记住。
这一段只是为了证明我们为什么可以直接将j移动到k而无须再比较前面的k个字符。
好,接下来就是重点了,怎么求这个(这些)k呢?因为在P的每一个位置都可能发生不匹配,也就是说我们要计算每一个位置j对应的k,所以用一个数组next来保存,next[j] = k,表示当T[i] != P[j]时,j指针的下一个位置。
以上文章摘自该博文
对于模式串求next数组 便能够每次只进行模式串指针的移动
对于next的求解过程
next[0] = -1 next[1] = 0;
当str[j] == str[k] 时 next[j + 1] = next[j] + 1;
当不相等时 我们让k指针往前蹦 蹦到头或者相等为止
这样做的目的就是尽可能的使其能够与主串j之前的更多的字母匹配
然后kmp部分 就好说了 每次i不动 只移动j指针就好了
标签:
原文地址:http://www.cnblogs.com/zhanzhao/p/4760916.html