标签:
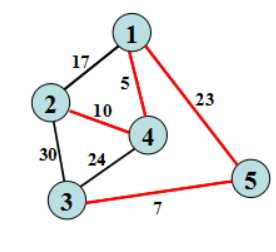
现在再谈最小生成树: 含有n个结点的图,从中选n-1条边,保持n-1个点中任意两点是连通的,并且n-1条边的和最小。这n个点和这n-1条边就成为原图的最小生成树。
第一个算法和Dijstra相似,请点击链接:http://www.cnblogs.com/ZZMbk/p/4761608.html
第二个算法要用到并查集,请点击链接:http://www.cnblogs.com/ZZMbk/p/4759952.html
①.Prim
任意结点开始(不妨设为v1)构造最小生成树: 首先把这个结点包括进生成树里,然后在那些其一个端点已在生成树里、另一端点还未在生成树里的所有边中找出权值最小的一条边,并把这条边、包括不在生成树的另一端点包括进生成树,…。依次类推,直至将所有结点都包括进生成树为止。
堆优化时,储存两个数据:一条边权值(唯一和dijstra有区别的地方),和点编号
由于和Dijstra区别不大,直接给程序:
type point=^node; node=record val,q:longint; next:point; end; type arr=record bh,zhi:longint; end; var a:array[1..100000]of point; head,p:point; n,m,i,j,x,y,ans,dans,t,q:longint; dui:array[1..100000]of arr; f:array[1..100000]of longint; used:array[1..100000]of boolean; procedure swap(var a,b:arr); var t:arr; begin t:=a;a:=b;b:=t; end; procedure up(k:longint); var p:longint; begin p:=k; if p=1 then exit; while dui[p].zhi<dui[p div 2].zhi do begin swap(dui[p],dui[p div 2]); p:=p div 2; if p=1 then break; end; end; procedure down; var p,min,minw:longint; begin p:=1; if p*2>dans then exit; if p*2=dans then begin min:=dui[p*2].zhi;minw:=p*2; end else if dui[p*2].zhi<dui[p*2+1].zhi then begin min:=dui[p*2].zhi;minw:=p*2; end else begin min:=dui[p*2+1].zhi;minw:=p*2+1; end; while dui[p].zhi>min do begin swap(dui[p],dui[minw]); p:=minw; if p*2>dans then break; if p*2=dans then begin min:=dui[p*2].zhi;minw:=p*2; end else if dui[p*2].zhi<dui[p*2+1].zhi then begin min:=dui[p*2].zhi;minw:=p*2; end else begin min:=dui[p*2+1].zhi;minw:=p*2+1; end; end; end; begin assign(input,‘Prim.in‘); assign(output,‘Prim.out‘); reset(input);rewrite(output); readln(n,m); for i:=1 to n do begin used[i]:=false;f[i]:=maxlongint; end; for i:=1 to m do begin readln(x,y,j); new(p);p^.val:=j;p^.q:=y;p^.next:=a[x];a[x]:=p; new(p);p^.val:=j;p^.q:=x;p^.next:=a[y];a[y]:=p; end; dui[1].bh:=1;dui[1].zhi:=0;dans:=1; f[1]:=0;used[1]:=true; ans:=0; q:=0; while dans<>0 do begin t:=dui[1].bh; head:=a[t]; used[t]:=true; ans:=ans+f[t]; while head<>nil do begin if (not used[head^.q])and(head^.val<f[head^.q]) then begin inc(dans);dui[dans].bh:=head^.q;dui[dans].zhi:=head^.val; up(dans); f[head^.q]:=head^.val; end; head:=head^.next; end; while used[dui[1].bh] do begin dui[1].zhi:=dui[dans].zhi;dui[1].bh:=dui[dans].bh; dec(dans);if dans<=0 then break; down; end; end; writeln(ans); close(input);close(output); end.
②.Kruskal:
算法步骤:
1、把图中的边按权值从小到大排序。
2、按从小到大的顺序依次向树中加边。 在添加每一条边(u,v)时,如果u和v两个点在同一集 合中,一旦添加,就回构成回路,所以放弃该边,在向后找下一条边。
3、直到添加n-1条边。
关键:加边时不能构成回路:边的两个顶点是否已在树中。
type arr=record u1,u2,v:longint; end;//u1,u2是两个顶点,v是两个顶点所连的边的权值 var e:array[1..100000]of arr;//边 fa:array[1..100000]of longint; n,m,x,y,i,j,ans:longint; procedure qsort(l,r:longint); var i,j,mid:longint; t:arr; begin i:=l;j:=r; mid:=e[(l+r) div 2].v; repeat while e[i].v<mid do inc(i); while e[j].v>mid do dec(j); if i<=j then begin t:=e[i];e[i]:=e[j];e[j]:=t; inc(i);dec(j); end; until i>j; if i<r then qsort(i,r); if l<j then qsort(l,j); end;//将所有的边进行快排 function find(x:longint):longint; begin if fa[x]=x then exit(x) else fa[x]:=find(fa[x]); exit(fa[x]); end;//并查集的查询操作 begin assign(input,‘Kruskal.in‘); assign(output,‘Kruskal.out‘); reset(input);rewritE(output); readln(n,m);ans:=0; for i:=1 to n do fa[i]:=i;for i:=1 to m do readln(e[i].u1,e[i].u2,e[i].v); qsort(1,m); for i:=1 to m do begin x:=find(e[i].u1); y:=find(e[i].u2); if x<>y then begin fa[x]:=y; ans:=ans+e[i].v; end;//合并操作由于太短,且只要用一次,所以没打过程
//若两个点不在同一集合,就用这条边 end; writeln(ans); close(input);close(output); end.
总结,因为即使优化后的Prim时间效率都和Kruskal时间效率同为O(m* log n),而Kruskal算法
短小精悍,所以果断使用Kruskal。这体现出并查集短小的优势!
标签:
原文地址:http://www.cnblogs.com/ZZMbk/p/4761704.html