标签：acm   动态规划   

题目：

Gray code

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only onebit (binary digit). The reflected binary code was originally designed to prevent spurious output from electromechanical switches. Today, Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.



Now , you are given a binary number of length n including ‘0’ , ’1’ and ‘?’(? means that you can use either 0 or 1 to fill this position) and n integers(a1,a2,….,an) . A certain binary number corresponds to a gray code only. If the ith bit of this gray code is 1,you can get the point ai.
Can you tell me how many points you can get at most?

For instance, the binary number “00?0” may be “0000” or “0010”,and the corresponding gray code are “0000” or “0011”.You can choose “0000” getting nothing or “0011” getting the point a3 and a4.

2
00?0
1 2 4 8
????
1 2 4 8

Case #1: 12
Case #2: 15
Hint
https://en.wikipedia.org/wiki/Gray_code

http://baike.baidu.com/view/358724.htm
 

题意：给一个n位二进制数，有一些位告诉了，有一些位不确定，把它转化为格雷码后为1的位置获得对应位置的分数，问最多得多少分。

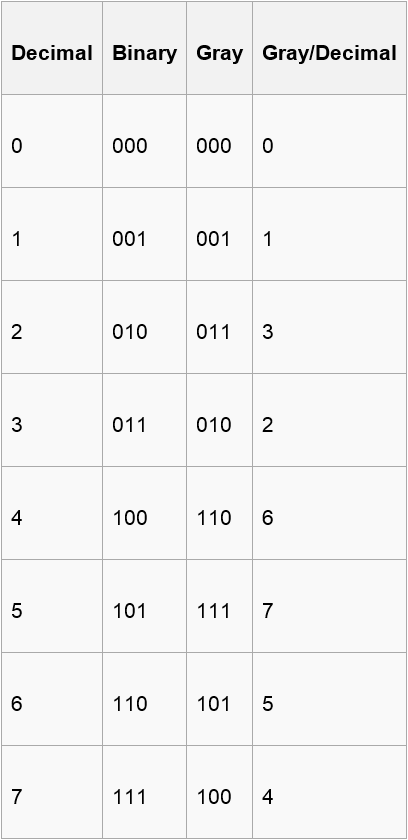
思路：二进制转格雷码的公式为G[0]=B[0],G[i]=B[i]^B[i-1]，所以当二进制第i位取值和第i-1位取值不同时，G[i]=1，可以得到A[i],否则G[i]=0,不能得到分数，DP方程为dp[i][0]=max(dp[i-1][0],dp[i-1][1]+a[i]),dp[i][1]=max(dp[i-1][1],dp[i-1][0]+a[i]),最终的结果为max(dp[n-1][1],dp[n-1][0]).

代码：

#include <cstdlib>
#include <cctype>
#include <cstring>
#include <cstdio>
#include <cmath>
#include<climits>
#include <algorithm>
#include <vector>
#include <string>
#include <iostream>
#include <sstream>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <fstream>
#include <numeric>
#include <iomanip>
#include <bitset>
#include <list>
#include <stdexcept>
#include <functional>
#include <utility>
#include <ctime>
using namespace std;

#define PB push_back
#define MP make_pair

#define REP(i,x,n) for(int i=x;i<(n);++i)
#define FOR(i,l,h) for(int i=(l);i<=(h);++i)
#define FORD(i,h,l) for(int i=(h);i>=(l);--i)
#define SZ(X) ((int)(X).size())
#define ALL(X) (X).begin(), (X).end()
#define RI(X) scanf("%d", &(X))
#define RII(X, Y) scanf("%d%d", &(X), &(Y))
#define RIII(X, Y, Z) scanf("%d%d%d", &(X), &(Y), &(Z))
#define DRI(X) int (X); scanf("%d", &X)
#define DRII(X, Y) int X, Y; scanf("%d%d", &X, &Y)
#define DRIII(X, Y, Z) int X, Y, Z; scanf("%d%d%d", &X, &Y, &Z)
#define OI(X) printf("%d",X);
#define RS(X) scanf("%s", (X))
#define MS0(X) memset((X), 0, sizeof((X)))
#define MS1(X) memset((X), -1, sizeof((X)))
#define LEN(X) strlen(X)
#define F first
#define S second
#define Swap(a, b) (a ^= b, b ^= a, a ^= b)
#define Dpoint  strcut node{int x,y}
#define cmpd int cmp(const int &a,const int &b){return a>b;}

 /*#ifdef HOME
    freopen("in.txt","r",stdin);
    #endif*/
const int MOD = 1e9+7;
typedef vector<int> VI;
typedef vector<string> VS;
typedef vector<double> VD;
typedef long long LL;
typedef pair<int,int> PII;
//#define HOME

int Scan()
{
	int res = 0, ch, flag = 0;

	if((ch = getchar()) == '-')				//判断正负
		flag = 1;

	else if(ch >= '0' && ch <= '9')			//得到完整的数
		res = ch - '0';
	while((ch = getchar()) >= '0' && ch <= '9' )
		res = res * 10 + ch - '0';

	return flag ? -res : res;
}
/*----------------PLEASE-----DO-----NOT-----HACK-----ME--------------------*/



char str[200000+5];
int a[200000+5];
 int dp[200000][2];
int main()
{int T;
RI(T);
for(int t=1;t<=T;t++)
{
    scanf("%s",str);
    int n=strlen(str);
    for(int i=0;i<n;i++)
        RI(a[i]);
    MS1(dp);
    if(str[0]=='?')
    {
        dp[0][0]=0;
        dp[0][1]=a[0];
    }
    else
        if(str[0]=='1')
    {
        //dp[0][0]=0;
        dp[0][1]=a[0];
    }
    else
    {
        dp[0][0]=0;
    }
    for(int i=1;i<n;i++)
    {
        if(str[i]=='0')
        {  int temp=-1;
           if(dp[i-1][1]!=-1)
            temp=max(temp,dp[i-1][1]+a[i]);
           if(dp[i-1][0]!=-1)
            temp=max(temp,dp[i-1][0]);
           dp[i][0]=temp;
        }
        else
            if(str[i]=='1')
        {
            int temp=-1;
           if(dp[i-1][0]!=-1)
            temp=max(temp,dp[i-1][0]+a[i]);
           if(dp[i-1][1]!=-1)
            temp=max(temp,dp[i-1][1]);
           dp[i][1]=temp;
        }
        else
            if(str[i]=='?')
        {
            int temp=-1;
           if(dp[i-1][1]!=-1)
            temp=max(temp,dp[i-1][1]+a[i]);
           if(dp[i-1][0]!=-1)
            temp=max(temp,dp[i-1][0]);
           dp[i][0]=temp;
             temp=-1;
           if(dp[i-1][0]!=-1)
            temp=max(temp,dp[i-1][0]+a[i]);
           if(dp[i-1][1]!=-1)
            temp=max(temp,dp[i-1][1]);
           dp[i][1]=temp;

        }
    }
    int sum=max(dp[n-1][0],dp[n-1][1]);
    printf("Case #%d: %d\n",t,sum);

}


        return 0;
}

hdu5375 Gray code(动态规划)

标签：acm   动态规划   

原文地址：http://blog.csdn.net/u013840081/article/details/48011833