整数拆分问题(从O(n^2优化到O(n*sqrt(n))

　1. 将n划分成若干正整数之和的划分数。
　　2. 将n划分成k个正整数之和的划分数。
　　3. 将n划分成最大数不超过k的划分数。
　　4. 将n划分成若干奇正整数之和的划分数。
　　5. 将n划分成若干不同整数之和的划分数。

1.将n划分成不大于m的划分法：
　　1).若是划分多个整数可以存在相同的：
　　 dp[n][m]= dp[n][m-1]+ dp[n-m][m] dp[n][m]表示整数 n 的划分中，每个数不大于 m 的划分数。
　　则划分数可以分为两种情况:
　　a.划分中每个数都小于 m，相当于每个数不大于 m- 1, 故划分数为 dp[n][m-1].
　　 b.划分中有一个数为 m. 那就在 n中减去 m ,剩下的就相当于把 n-m 进行划分， 故划分数为 dp[n-m][m];
　　2).若是划分多个不同的整数：
　　dp[n][m]= dp[n][m-1]+ dp[n-m][m-1] dp[n][m]表示整数 n 的划分中，每个数不大于 m 的划分数。
　　 同样划分情况分为两种情况：
　　a.划分中每个数都小于m,相当于每个数不大于 m-1,划分数为 dp[n][m-1].
　　b.划分中有一个数为 m.在n中减去m,剩下相当对n-m进行划分，
　　　并且每一个数不大于m-1，故划分数为 dp[n-m][m-1]
　　2.将n划分成k个数的划分法：
　　　　dp[n][k]= dp[n-k][k]+ dp[n-1][k-1];
　　方法可以分为两类：
　　　　第一类: n 份中不包含 1 的分法，为保证每份都 >= 2，可以先拿出 k 个 1 分
　　到每一份，然后再把剩下的 n- k 分成 k 份即可，分法有: dp[n-k][k]
　　 　　第二类: n 份中至少有一份为 1 的分法，可以先那出一个 1 作为单独的1份，剩
　　下的 n- 1 再分成 k- 1 份即可，分法有：dp[n-1][k-1]
　　
　　3.将n划分成若干奇数的划分法：（不懂）
　　　　g[i][j]:将i划分为j个偶数
　　　　f[i][j]:将i划分为j个奇数
　　 g[i][j] = f[i - j][j];
　　f[i][j] = f[i - 1][j - 1] + g[i - j][j];

以下给出O(n^2)算法

/*对于输入的 n,k; 
第一行： 将n划分成若干正整数之和的划分数。 
第二行： 将n划分成k个正整数之和的划分数。 
第三行： 将n划分成最大数不超过k的划分数。 
第四行： 将n划分成若干个 奇正整数之和的划分数。 
第五行： 将n划分成若干不同整数之和的划分数。 
第六行： 打印一个空行*/  
#include<iostream>  
#include <cstring>  
#include<vector>  
#include <cstdio>  
using namespace std;  
#define N 55+1  
int dp[N][N];  

int main()  
{  
    //分为若干个正整数和  
    //memset(dp,0,sizeof(dp));  
    int n,k;  
    int out[6];  
    while(cin>>n>>k)  
    {  
        memset(dp,0,sizeof(dp));  
        //任意个正整数和，则dp[i][j]表示i分解成最大不超过j的个数，  
        //分为最大是j和最大不是j，则dp[i][j]=dp[i-j][j]+dp[i][j-1];  
        dp[0][0]=1;  
        for (int i=0;i<=n;i++)  
        {  
            for (int j=1;j<=n;j++)  
            {  
                if(j<=i)  
                dp[i][j]=dp[i-j][j]+dp[i][j-1];  
                else  
                dp[i][j]=dp[i][i];  
            }  
        }  
        out[1]=dp[n][n];  
        out[3]=dp[n][k];  
        //分成K个正整数的和 ,分为k个数中没有1，和有1，  
        //dp[i][j],将i划分为j个dp[i][j]=dp[i-j][j]+dp[i-1][j-1];  
        memset(dp,0,sizeof(dp));  
        for(int i=1;i<=n;i++)  
        for (int j=1;j<=i;j++)  
        {  
              if(j==1)  
              dp[i][j]=1;  
              else  
              dp[i][j]=dp[i-j][j]+dp[i-1][j-1];   
        }  
        out[2]=dp[n][k];  
       //奇数和dp[i][j]为划分最大的奇数不超过j的数，  
       //则dp[i][j]=dp[i-n(j)][j]+dp[i][j-2];n(j)为不超过j的最大奇数  
       //初始条件，dp[i][1]=1,j为偶数时候dp[i][j]=dp[i][j-1];当i==n(j) ,  
       //出现dp[0][j]，也就是当i为奇数时候，dp[0][j]=1;  
       memset(dp,0,sizeof(dp));  
       for(int i=0;i<=n;i++)  
       {  
           dp[i][1]=1;  
           if(i&1)  
           dp[0][i]=1;  
        }  
        for (int i=1;i<=n;i++)  
        {  
            for (int j=1;j<=n;j++)  
            {  
                if(j&1)  
                {  
                    if(j<=i)  
                    dp[i][j]=dp[i-j][j]+dp[i][j-1];  
                    else   
                    dp[i][j]=dp[i][i];  
                }  
                else  
                dp[i][j]=dp[i][j-1];  
            }  
        }  
        out[4]=dp[n][n];  
//不同正整数和，dp[i][j]是不超过j的不同的整数和，dp[i][j]=dp[i-j][j-1]+dp[i][j-1];初始状态dp[1][1]=1;  
//当i==j时，出现dp[0][j-1],表示先拿出一个j出来，这时候就应该是1中情况。  

        memset(dp,0,sizeof(dp));  
        dp[0][0]=1;  
        for (int i=0;i<=n;i++)  
        {  
              for (int j=1;j<=n;j++)  
              {  
                   if(j<=i)  
                   dp[i][j]=dp[i-j][j-1]+dp[i][j-1];  
                    else  
                    dp[i][j]=dp[i][i];  
              }  
        }  
        out[5]=dp[n][n];  
        for (int i=1;i<=5;i++)  
            {  
                cout<<out[i]<<endl;  
            }  
            cout<<endl;  

       }  
}     

但我在做51nod的时候发现数据给的范围很大(5*10^4)，这种方法不仅内存存不下，而且还TLE

下面给出n个数拆成不同数的方案的O(nsqrt(n))算法

dp[i][j]代表i个数相加等于j
由于有不同的数最多不超过O(sqrt(n))算法个，则可以优化

dp[i][j] = dp[i-1][j-i] + dp[i][j-i]

这个递推方程的转移含义是i-1个数每个数都加1,最后再添上一个1，就从dp[i-1][j-i]转到dp[i][j],还有就是i个数每个数都加1，就从dp[i][j-i]转到dp[i][j]

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
#include <cmath>

int dp[600][51000];
int const mod = 1e9+7;
using namespace std;
int main()
{

  int n;
  while(scanf("%d",&n) != EOF){
     dp[0][0] = 1;
      for(int i =1; i <= 2*(int)sqrt(n); i++ )
      {
          for(int j = 0; j <= n; j++)
          {
              dp[i][j] = (dp[i-1][j-i] + dp[i][j-i])%mod;
          }
      }

      int ans = 0;
      for(int i =1; i <= 2*(int)sqrt(n); i++ )
      {
          ans += dp[i][n];
          ans %= mod;
      }
          printf("%d\n",ans);
  }

  return 0;
}

那么当将n划分成若干正整数之和的划分数呢？
可以相同，那么上面那个方法就不行了
可以用5边形数来求
参考资料
https://en.wikipedia.org/wiki/Partition_(number_theory)

用一个公式就行

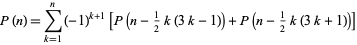
其中n-k*(3*k-1)/2>=0,n-k*(3*k+1)/2>=0；
注意两个条件要分开判断，有大于0的就加上相应的f，不是两个同时成立或者不成立

这个公式的时间复杂度是O(n^1.5)

#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;

long long tar[100002];
const int MOD=1000000007;

void init()
{
    memset(tar,0,sizeof(tar));
    tar[0]=1;

    for(int i=1;i<=50000;i++)
    {
        int nbit;
        for(int j=1;;j++)
        {
            int element1,element2;
            element1=i-j*(3*j-1)/2;
            element2=i-j*(3*j+1)/2;
            if(j&1)
                nbit=1;
            else if(j%2==0)
                nbit=-1;

            if(element2<0 && element1<0)
                break;

            if(element1>=0)
            {
                tar[i]=(tar[i]+nbit*tar[element1])%MOD;
            }
            if(element2>=0)
            {
                tar[i]=(tar[i]+nbit*tar[element2])%MOD;
            }
        }
        tar[i]=(tar[i]+MOD)%MOD;
    }


}

int main()
{

    init();
    int rat;
    while(cin>>rat)
    {

        cout<<tar[rat]<<endl;
    }
    return 0;
}

计算机是人造学科，数学是神造学科！！！orz….