标签：c   图论   网络流   

Going Home

On a grid map there are n little men and n houses. In each unit time, every little man can move one unit step, either horizontally, or vertically, to an adjacent point. For each little man, you need to pay a $1 travel fee for every step he moves, until he enters a house. The task is complicated with the restriction that each house can accommodate only one little man.

Your task is to compute the minimum amount of money you need to pay in order to send these n little men into those n different houses. The input is a map of the scenario, a ‘.‘ means an empty space, an ‘H‘ represents a house on that point, and am ‘m‘ indicates there is a little man on that point.

You can think of each point on the grid map as a quite large square, so it can hold n little men at the same time; also, it is okay if a little man steps on a grid with a house without entering that house.

2 2
.m
H.
5 5
HH..m
.....
.....
.....
mm..H
7 8
...H....
...H....
...H....
mmmHmmmm
...H....
...H....
...H....
0 0

2
10
28

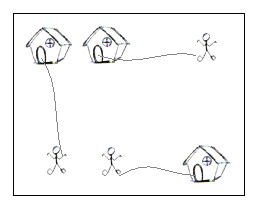
一个N*M地图上有相同数量的字符H和字符m，m代表一个 人，H代表一个房子。人到房子的花销是它们在图中的曼哈顿距离，问你让所有人回到房子所需要的最小费用（一个房子只能容纳一个人）。

解题：

第一道最小费用流的题，没敢写难题，选了个裸题来A，感谢斌神的模板， 感谢小B的解析。

因为是裸题，思路还是比较好想的，简单说一下建图思路：

（1）建立超级源点outset， 超级汇点inset。

（2）源点向每个人建边， 容量为1， 费用为0。

（3）房子向汇点建边，容量为1， 费用为0。

（4）每个人和房子建边，容量为1，费用为曼哈顿距离。

从outset到inset跑一遍最小费用最大流就行了

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define INF 0x3f3f3f3f
#define maxn 220
#define maxm 88000
using namespace std;
int n, m;
int outset;//超级源点
int inset;//超级汇点
struct node {
    int u, v, cap, flow, cost, next;
};

node edge[maxm];
int head[maxn], cnt;
int per[maxn];//记录增广路径上 到达点i的边的编号
int dist[maxn], vis[maxn];

void init(){
    cnt = 0;
    memset(head, -1, sizeof(head));
}

void add(int u, int v, int w, int c){
    edge[cnt] = {u, v, w, 0, c, head[u]};
    head[u] = cnt++;
    edge[cnt] = {v, u, 0, 0, -c, head[v]};
    head[v] = cnt++;
}

int dir(int x1, int y1, int x2, int y2){
    return abs(x1 - x2) + abs(y1 - y2);
}

struct NODE{
    int x, y;
};

NODE maph[maxn], mapm[maxn];
int ans_h, ans_m;

void getmap(){
    char str[120][120];
    ans_h = ans_m = 0;
    for(int i = 0; i < n; ++i){
        scanf("%s", str[i]);
        for(int j = 0; j < m; ++j){
            if(str[i][j] == 'm'){
                ans_m++;
                mapm[ans_m].x = i;
                mapm[ans_m].y = j;
            }
            if(str[i][j] == 'H'){
                ans_h++;
                maph[ans_h].x = i;
                maph[ans_h].y = j;
            }
        }
    }
    int t = ans_h;//人数
    outset = 0;//源点
    inset = t * 2 + 1;//汇点
    for(int i = 1; i <= t; ++i){
        add(outset, i, 1, 0);
        add(i + t, inset, 1, 0);
        for(int j = 1; j <= t; ++j){
            int d = dir(maph[i].x, maph[i].y, mapm[j].x, mapm[j].y);
            add(i, j + t, 1, d);
        }
    }
}
//寻找花销最小的路径
//跑一遍SPFA 找st——ed的最少花销路径 且该路径上每一条边不能满流
//若存在 说明可以继续增广，反之不能
bool SPFA(int st, int ed){
    queue<int>q;
    memset(dist, INF, sizeof(dist));
    memset(vis, 0, sizeof(vis));
    memset(per, -1, sizeof(per));
    dist[st] = 0;
    vis[st] = 1;
    q.push(st);
    while(!q.empty()){
        int u = q.front();
        q.pop();
        vis[u] = 0;
        for(int i = head[u]; i != -1; i = edge[i].next){
            node E = edge[i];
            if(dist[E.v] > dist[u] + E.cost && E.cap > E.flow){//可以松弛 且 没有满流
                dist[E.v] = dist[u] + E.cost;
                per[E.v] = i;//记录到达这个点的边的编号
                if(!vis[E.v]){
                    vis[E.v] = 1;
                    q.push(E.v);
                }
            }
        }
    }
    return per[ed] != -1;
}

void MCMF(int st, int ed, int &cost, int &flow){
    flow = 0;//总流量
    cost = 0;//总费用
    while(SPFA(st, ed)){//每次寻找花销最小的路径
        int mins = INF;
        //通过反向弧 在源点到汇点的最少花费路径 找最小增广流
        for(int i = per[ed]; i != -1; i = per[edge[i ^ 1].v]){
            mins = min(mins, edge[i].cap - edge[i].flow);
        }
         //增广
        for(int i = per[ed]; i != -1; i = per[edge[i ^ 1].v]){
            edge[i].flow += mins;
            edge[i ^ 1].flow -= mins;
            cost += edge[i].cost * mins;//增广流的花销
        }
        flow += mins//总流量累加
    }
}
int main (){
    while(scanf("%d%d", &n, &m), n || m){
        init();
        getmap();
        int cost, flow;//最小费用 最大流
        MCMF(outset,inset, cost, flow);
        printf("%d\n", cost);
    }
    return 0;
}

HDU 1533--Going Home【最小费用最大流 && 模板】

标签：c   图论   网络流   

原文地址：http://blog.csdn.net/hpuhjh/article/details/48035993