灰色系统理论与应用

标签：

　　现实生活中的很多实际问题的内部结构，参数以及特征等并不是完全已知的，人们只能根据思维逻辑推断来构造模型研究。这种部分信息已知而部分信息未知的系统被称为灰色系统。作为实际问题的研究，灰色系统是最为常见，本文主要围绕灰色系统展开一系列的学习。

一 灰色系统概述

1.灰色系统

　　听到灰色系统，相信大家肯定会想为什么要是“灰色”系统，那是不是也有个白色、黑色系统？对，确实如此，白色系统用来指那些信息完备，发展变化规律明显，定量描述较方便，结构和参数较具体的系统；对应的黑色系统就是那些内部结构完全未知的系统。

　　作为实际问题，相对于白色和黑色系统，灰色系统是最为常见的。利用灰色系统理论建模来处理实际问题，主要任务是根据具体灰色系统的行为特征数据，充分开发并利用不多的数据中的显信息和隐信息， 寻找各因素间或因素本身的数学关系。

　　灰色系统可以理解为对客观系统进行新的认识，那怎么认识呢？我们知道，系统中的某些信息不够充分，但是作为系统必然是有特定功能和有序的，只是其内在规律并未充分外露，基于此，我们的目的就是发现；除此之外，在做系统研究时，一定会遇到一些随机的无规则的干扰成分以及杂乱无章的数据列，在灰色系统的观点之下，这些并不是不可捉摸的，灰色系统理论讲这些随机量看作是在一定范围变化的灰色量，相应的对原始数据加工处理，将灰色数变为生成数，根据生成数进而得到规律性较强的生成函数。

2. 关联分析

　　我们知道，在对社会、经济、农业以及生态系统等方面的研究时，都会有不可忽略的“噪声”（随机干扰），受随机干扰的系统理论主要立足于概率统计。回归分析是现有的统计分析中最常用的一种方法，但其具有不可避免的三大缺陷：（1）要求大样本，只有通过大量数据才能量化得到规律；（2）要求样本有较好的分布规律，而很多实际情况并非如此；（3）不能分析因素间动态的关联程度，在处理问题上的精度并不是很高。

　　针对于回归分析的欠缺，灰色系统提出了一种新的分析方法—关联分析方法，根据因素之间发展态势的相似或相异程度来衡量因素间关联的程度。该方法以发展态势为立足点，对样本的多少没有过分要求，也不再需要典型的分布规律。作为一个发展变化的系统，关联分析实际上是动态过程发展态势的量化比较分析。

　　实际问题通常具有不同的量纲，关联分析中，为了保证建模的质量和系统分析的正确结果，对收集来的原始数据必须进行相应的数据变换，使其消除量纲和具有可比性，具体的方法如下：

　　设有序列x = (x(1),x(2),…,x(n))

　　则称映射f:x->y       f(x(k)) = y(k) , k = 1,2,…,n为序列x到序列y的数据变化。

相应的对序列做如下变换：

（1）初值变换：用y(k) = x(k)/x(1)，其中x(1)!=0

（2）均值变换：y(k) = x(k)/x的均值

（3）百分比变换：y(k) = x(k)/max x(k)

（4）倍数变换：y(k) = x(k)/min x(k)

（5）归一化变化：y(k) = x(k)/x0，其中x0为大于零的某个值

（6）极差最大值化变换：y(k) = (x(k) – min x(k))/max x(k)

（7）间值化变换：y(k) = (x(k) – min x(k)) / (max x(k) – min x(k))

下来对比较数列x_i参考数列x₀在k时刻的关联分析：

选取参考数列x₀ = {x₀(1),x₀(2),...,x₀(n)),其中k表示时刻。假定有m个比较数列：x_i = {x_i(1),x_i(2),...,x_i(m)).

则称：

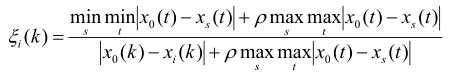
为比较数列对参考数列的关联系数，每个时刻都有一个关联数，其中ρ为分辨系数，越大表明分辨率越大。由于每个时刻都有一个关联数，显得过于分散且不便计算，故定义关联度：

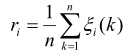
关联度将各个时刻的关联系数联系起来，据此我们可以对各个问题进行因素分析。 

在对问题进行关联分析时，首先对各个数据进行无量纲化，进而进行关联分析，在采用关联分析时的MATLAB程序为：

clc,clear
load x.txt %把原始数据存放在纯文本文件 x.txt 中，其中把数据的"替换替换成.
for i=1:15
　　x(i,:)=x(i,:)/x(i,1); %标准化数据
end
for i=16:17
　　x(i,:)=x(i,1)./x(i,:); %标准化数据
end
data=x;
n=size(data,2); %求矩阵的列数，即观测时刻的个数
ck=data(1,:); %提出参考数列
bj=data(2:end,:); %提出比较数列
m2=size(bj,1); %求比较数列的个数
for j=1:m2
　　t(j,:)=bj(j,:)-ck;
end

mn=min(min(abs(t‘))); %求最小差
mx=max(max(abs(t‘))); %求最大差
rho=0.5; %分辨系数设置
ksi=(mn+rho*mx)./(abs(t)+rho*mx); %求关联系数
r=sum(ksi‘)/n %求关联度
[rs,rind]=sort(r,‘descend‘) %对关联度进行排序

当参考数列不止一个，被比较的元素不止一个时，需要进行优势分析。可以构造各个参考数列对比较因素的关联度矩阵，根据矩阵中元素的大小，确定元素所起的作用，这种分析叫做优势分析。

3.生成数

　　之前说过，面对各种系统中的随机干扰现象，大多的研究都是基于概率统计方法，但概率统计要求大量数据、典型的统计规律，但有些问题的概率结论是毫无意义的，比如预报某天下雨和晴天的概率均为0.5。

　　灰色系统把一切随机量看作是灰色数，对灰色数的处理不是找寻概率分布，而是利用数据处理的办法去寻找数据之间的规律。通过对数列中的数据进行处理，产生新的数列，以此来挖掘和寻找数的规律性的方法，叫做数的生成。数的生成方式有多种：累加生成、累减生成以及加权累加等等。

（1）累加生成

　　将数列各时刻的数据依次累加的过程叫做累加过程，记作AGO，累加生成的新数列，叫做累加生成数列，原数列记为：x⁰ = (x⁰(1),x⁰(2),…,x⁰(n))，累加生成数列记为：x¹ = (x¹(1),x¹(2),…x¹(n))，满足：　　　　

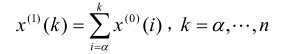
其中上标1表示一次累加生成，相应的将一次累加生成结果作为原始数列，得到的累加生成数列为2此累加生成，同理可推出n次累加生成。在实际应用中，最常用的还是一次累加生成。 

（2）累减生成

　　利用数的生成可得到一系列有规律的数据，加以利用，但是生成的数不一定全是直接可用的数列，这就需要对生成数进行还原。那么对于累加生成而言，还原采用累减生成，与累加生成所不同的是将求和转化为求差，记为IAGO。 

（3）均值生成

　　原数列记为：x⁰ = (x⁰(1),x⁰(2),…,x⁰(n))，则x⁰(k-1)与x⁰(k)为数列x⁰的一对紧邻值，x⁰(k-1)称为前值，x⁰(k)称为后值，对于常数a属于[0,1],则称Z⁰(k) = ax⁰(k) + (1 – a)x⁰(k -1)为由系数x⁰的邻值在生成系数a下的均值生成数，当a = 0.5时，对应的Z为紧邻均值生成数。

二 灰色模型GM以及灰色预测

　　灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程，进而用离散数据建立微分方程形式的动态模型，就是灰色模型，记为GM（Grey Model）。灰色模型是利用离散随机数经过生成变为随机性被削弱同时较有规律的生成数，建立起的微分方程形式的模型。 

1.GM模型

　　根据AGO生成数的定义，

原数列记为：x⁰ = (x⁰(1),x⁰(2),…,x⁰(n))，累加生成数列记为：x¹ = (x¹(1),x¹(2),…x¹(n))，满足：　　　　

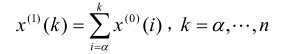则x1对应的灰导数为：dx¹(k) = x⁰(k) = x¹(k) – x¹(k-1)

令Z¹为数列x1的紧邻均值数列，则：

Z¹(k) = 0.5x¹(k) + 0.5x¹(k-1),其中k = 2,3,…,n

则，Z¹ = (Z¹(2),Z¹(3),…,Z¹(n))，对应的GM(1,1)的灰微分方程模型可定义为：

dx¹(k) + aZ¹(k) = b,即：x⁰(k) – aZ¹(k) = b,其中x0(k)为灰导数，a称为发展系数,Z¹(k)称为白化背景值，b称为灰作用量。

将k = 2,3,…,n代入上式，则有：

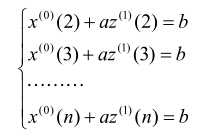
相应的，令：

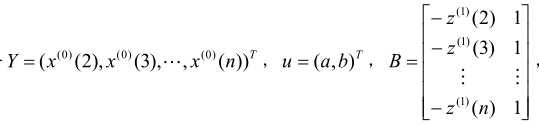
其中Y为数据向量，B为数据矩阵，u为参数向量，则GM（1,1）模型可表示为矩阵方程Y = Bu,根据最小二乘法可求得：　　　　

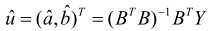
 GM(1,1) GM(1,1)表示的模型是1阶方程，只含有1个变量的灰色模型，而GM(1,N)表示的模型是1阶方程，但含有N个变量的灰色模型。

 2. 灰色预测

 灰色预测指的是利用GM模型对系统行为特征的发展变化规律进行预测估计，同时也可以对行为特征的异常情况做出研究等等。

1.灰色预测的方法

 设已知参考数列为x⁰ = (x⁰(1),x⁰(2),...,x⁰(n)),做AGO生成数列x¹ = (x¹(1),x¹(2),...,x¹(n)) = (x¹(1),x¹(1)+x⁰(2),...,x¹(n-1)+x⁰(n)),求均值数列z¹(k) = 0.5x¹(k) + 0.5x¹(k-1),k = 2,3,...,n。则z¹ =( z¹(2) ,z¹(3),...,z¹(n))。根据上述分析可以建立灰微分方程：x⁰(k) + az¹(k) = b，相应的白化方程为：dx¹/dt + ax¹(t) = b,通之前灰色模型中的计算方法，在这里可求得：x¹(k+1) = (x⁰(1) - b/a)e^-ak + b/a,k = 0,1,...,n-1。　　

2. 灰色预测的步骤：

（1）数据的检验与处理

　　为了保证建模方法的可行性，在建模之前，需要对原始数列做必要的检验处理，即计算数列的级比：λ(k) = x⁰(k-1)/x⁰(k),如果所有级比均落在(e^-2/(n+1),e^2/(n+2))内，则数列x⁰可以作为模型GM(1,1)对数据进行灰色预测，如不满足，则需要对原始数列做必要的变换处理，使其落在可溶范围内，一般取适当的常数c,做平移变换：

　　　　y⁰(k) = x⁰(k) + c,　　k = 1,2,...,n

则使数列y⁰ = (y⁰(1),y⁰(2),...,y⁰(n))的级比落在可容范围之内。

2. 预测模型

　　根据之前的预测方法建立模型GM(1,1),相应是我得到预测值：

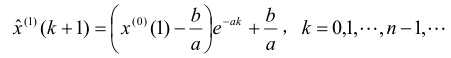
并有：　　　　　　　

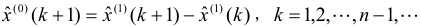
3. 检验预测值

（1）残差检验

残差的计算公式可定义为：

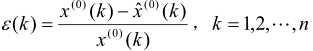
其中：，如果ε(k)<0.2,则可认为达到了一般要求，如果ε(k)<0.1,则认为达到了较高要求。

（2）级比偏差值检验

首先根据原始数列求出级比λ(k),结合发展系数a求出相应的级比偏差：ρ(k) = 1 - ((1-0.5a)/(1+0.5))λ(k),如果ρ(k)<0.2，则可认为达到了一般要求，如果ρ(k)<0.1,则认为达到了较高要求。

据此便可以利用灰色预测来实现对实际问题的求解，可以参考历年的数模试题中的预测类型进行分析总结。

灰色系统理论与应用

标签：

原文地址：http://www.cnblogs.com/ybjourney/p/4765948.html