标签:
一、01背包问题
01背包是在M件物品取出若干件放在空间为W的背包里,每件物品的体积为C1,C2,…,Cn,与之相对应的价值为W1,W2,…,Wn.求解将那些物品装入背包可使总价值最大。
动态规划:
1) 子问题定义:F[i][j]表示前i件物品中选取若干件物品放入剩余空间为j的背包中所能得到的最大价值。
2) 根据第i件物品放或不放进行决策
![]()
其中F[i-1][j]表示前i-1件物品中选取若干件物品放入剩余空间为j的背包中所能得到的最大价值;
而F[i-1][j-C[i]]+W[i]表示前i-1件物品中选取若干件物品放入剩余空间为j-C[i]的背包中所能取得的最大价值加上第i件物品的价值
根据第i件物品放或是不放确定遍历到第i件物品时的状态F[i][j]。
设物品件数为N,背包容量为V,第i件物品体积为C[i],第i件物品价值为W[i]。
由此写出伪代码如下:
1 F[0][] ← {0} 2 3 F[][0] ← {0} 4 5 for i←1 to N 6 7 do for k←1 to V 8 9 F[i][k] ← F[i-1][k] 10 11 if(k >= C[i]) 12 13 then F[i][k] ← max(F[i][k],F[i-1][k-C[i]]+W[i]) 14 15 return F[N][V]
上述代码9-13行也可以这样写:
if(k<C[i])//如果第i个物品的体积已经大于背包剩余容量 then F[i][k] ← F[i-1][k]
else F[i][k] ← max(F[i-1][k],F[i-1][k-C[i]]+W[i])
理解为:当第i个物品的体积大于背包剩余容量时,第i个物品肯定不能被放进去,所以F[i][k]=F[i-1][k],
而当第i个物品的体积小于或等于背包剩余容量时,可以有两种选择,放第i个物品(F[i-1][k-C[i]]+W[i])或者不放(F[i-1][k]),然后选择两者之间最优的。
而写成第一种等价的伪代码是为了更好的理解从二维数组解法到一维数组解法的转换。
根据算法求出的最大价值表本身其实含有位置信息,从F[N][V]逆着走向F[0][0],设i=N,j=V,如果F[i][j]==F[i-1][j-C[i]]+W[i]说明包里面有第i件物品,同时j -= C[i],不管F[i][j]与F[i-1][j-C[i]]+W[i]相不相等i都要减1,因为01背包的第i件物品要么放要么不放,不管放还是不放其已经遍历过了,需要继续往下遍历。
打印背包内物品的伪代码如下:
1 i←N 2 3 j←V 4 5 while(i>0 && j>0) 6 7 do if(F[i][j]=F[i-1][j-C[i]]+W[i]) 8 9 then Print W[i] 10 11 j←j-C[i] 12 13 i←i-1
也可以定义一个二维数组Path[N][V]来存放背包内物品信息,开始时Path[N][V]初始化为0,当 F[i][j]==F[i-1][j-C[i]]+W[i]时Path[i][j]置1。最后通过从Path[N+1][V+1]逆着走向Path[0][0]来获取背包内物品。其中Path[0][]与Path[][0]为边界。
加入路径信息的伪代码如下:
F[0][] ← {0} F[][0] ← {0} Path[][] ← 0 for i←1 to N do for k←1 to V F[i][k] ← F[i-1][k] if(k >= C[i] && F[i][k] < F[i-1][k-C[i]]+W[i]) then F[i][k] ← F[i-1][k-C[i]]+W[i] Path[i][k] ← 1 return F[N][V] and Path[][]
打印背包内物品的伪代码如下:
i←N
j←V
while(i>0 && j>0)
do if(Path[i][j] = 1)
then Print W[i]
j←j-C[i]
i←i-1
将使用二位数组改为使用一维数组:
观察伪代码可也发现,F[i][j]只与F[i-1][j]和F[i-1][j-C[i]]有关,即只和i-1时刻状态有关,所以我们只需要用一维数组F[]来保存i-1时的状态F[]。假设i-1时刻的F[]为{a0,a1,a2,…,av},难么i时刻的F[]中第k个应该为max(ak,ak-C[i]+W[i])即max(F[k],F[k-C[i]]+W[i]),这就需要我们遍历V时逆序遍历,这样才能保证求i时刻F[k]时F[k-C[i]]是i-1时刻的值。如果正序遍历则当求F[k]时其前面的F[0],F[1],…,F[K-1]都已经改变过,里面存的都不是i-1时刻的值,这样求F[k]时利用F[K-C[i]]必定是错的值。最后F[V]即为最大价值。
求F[j]的状态方程如下:

伪代码如下:
1 F[] ← {0} 2 3 for i ← 1 to N 4 5 do for k ← V to C[i] 6 7 F[k] ← max(F[k],F[k-C[i]]+W[i]) 8 9 return F[V]
加入路径信息的伪代码如下:
1 F[] ← {0} 2 3 Path[][]←0 4 5 for i←1 to N 6 7 do for k←V to C[i] 8 9 if(F[k] < F[k-C[i]]+W[i]) 10 11 then F[k] ← F[k-C[i]]+W[i] 12 13 Path[i][k] ← 1 14 15 return F[V] and Path[][]
二、物品无限的背包问题
将01背包一维数组解法中j的遍历顺序do for k←V to C[i]改为do for k←C[i] to V就变成了物品无限背包的解法。
1 F[] ← {0} 2 3 for i ← 1 to N 4 5 do for k ← C[i] to V 6 7 F[k] ← max(F[k],F[k-C[i]]+W[i]) 8 9 return F[V]
三、代码实际操练:
二维数组解法:
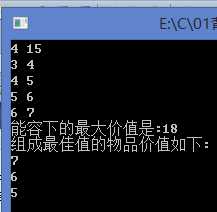
01背包问题具体例子:先输入两个数n,V表示物品的个数和背包的容量,接下来输入n组数据代表n种物品,每组数据有两个值对应物品的体积和价值,每种物品只有一个,求在背包容量下能装物品最大价值,并求出最大价值下,组合中各个物品的价值?
#include<iostream> using namespace std; const int N_max=100;//物品个数上限 const int V_max=100;//背包容量上限 int dp[N_max][V_max]; bool flag[N_max][V_max]; int main() { int n;//实际输入物品的个数 cin>>n; int V;//背包的实际容量 cin>>V; int *v=new int[n+1]; int *price=new int[n+1]; //输入n组数据,分别为体积v和价值price //注意这里要从1开始 for(int i=1;i<=n;i++) { cin>>v[i]>>price[i]; } //初始化dp数组 //注意这里的= for(int i=0;i<=n;i++) { dp[i][0]=0; } for(int i=0;i<=V;i++) { dp[0][i]=0; } //初始化flag数组 memset(flag,false,(n+1)*(V+1)*sizeof(bool)); //开始递推 for(int i=1;i<=n;i++) { for(int j=1;j<=V;j++) { dp[i][j]=dp[i-1][j]; if(v[i]<=j && dp[i-1][j-v[i]]+price[i]>dp[i][j])//放下该物品 { dp[i][j]=dp[i-1][j-v[i]]+price[i]; flag[i][j]=true; } } } cout<<"能容下的最大价值是:"<<dp[n][V]<<endl; cout<<"组成最佳值的物品价值如下:"<<endl; int i=n; int j=V; while(i>=0 && j>=0) { if(flag[i][j]) { cout<<price[i]<<endl; j=j-v[i]; } i--; } return 0; }
一维数组的解法:
#include<iostream> using namespace std; bool flag[100][100]={false}; int main() { int n;//实际输入物品的个数 cin>>n; int V;//背包的实际容量 cin>>V; int *dp=new int[V+1]; int *v=new int[n+1]; int *price=new int[n+1]; //输入n组数据,分别为体积v和价值price //注意这里要从1开始 for(int i=1;i<=n;i++) { cin>>v[i]>>price[i]; } //初始化dp数组 memset(dp,0,(V+1)*sizeof(int)); //开始递推 for(int i=1;i<=n;i++) { for(int j=V;j>=v[i];j--) //for(int j=v[i];j<=V;j++) { if( dp[j-v[i]]+price[i]>dp[j])//放下该物品 { dp[j]=dp[j-v[i]]+price[i]; flag[i][j]=true; } } } cout<<"能容下的最大价值是:"<<dp[V]<<endl; cout<<"组成最佳值的物品价值如下:"<<endl; int i=n; int j=V; while(i>=0 && j>=0) { if(flag[i][j]) { cout<<price[i]<<endl; j=j-v[i]; } i--; } return 0; }
调试结果:
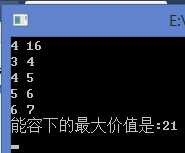
物品无限背包问题具体例子:先输入两个数n,V表示物品的个数和背包的容量,接下来输入n组数据代表n种物品,每组数据有两个值对应物品的体积和价值,每种物品有无限个,求在背包容量下能装物品最大价值,并求出最大价值下,组合中各个物品的价值?
#include<iostream> #include<algorithm> #include<vector> using namespace std; bool flag[100][100]={false}; int main() { int n;//实际输入物品的个数 cin>>n; int V;//背包的实际容量 cin>>V; int *dp=new int[V+1]; int *v=new int[n+1]; int *price=new int[n+1]; //输入n组数据,分别为体积v和价值price //注意这里要从1开始 for(int i=1;i<=n;i++) { cin>>v[i]>>price[i]; } //初始化dp数组 memset(dp,0,(V+1)*sizeof(int)); //开始递推 for(int i=1;i<=n;i++) { for(int j=v[i];j<=V;j++) { if( dp[j-v[i]]+price[i]>dp[j])//放下该物品 { dp[j]=dp[j-v[i]]+price[i]; flag[i][j]=true; } } } cout<<"能容下的最大价值是:"<<dp[V]<<endl; return 0; }
标签:
原文地址:http://www.cnblogs.com/bewolf/p/4776880.html