hdu 1204 糖果大战

标签：

Problem Description

生 日Party结束的那天晚上，剩下了一些糖果，Gandon想把所有的都统统拿走，Speakless于是说：“可以是可以，不过我们来玩24点，你不是 已经拿到了一些糖果了吗？这样，如果谁赢一局，就拿走对方一颗糖，直到拿完对方所有的糖为止。”如果谁能算出来而对方算不出来，谁就赢，但是如果双方都能 算出或者都不能，就算平局，不会有任何糖果的得失。
Speakless是个喜欢提前想问题的人，既然他发起了这场糖果大战，就自然很想赢啦（不然可就要精光了-_-）。现在他需要你的帮忙，给你他每局赢的概率和Gardon每局赢的概率，请你给出他可能获得这场大战胜利的概率。

Input

每行有四个数，Speakless手上的糖果数N、Gardon手上的糖果数M(0<=N,M<=50)、一局Speakless能解答出来的概率p、一个问题Gardon能解答出来的概率q(0<=p,q<=1)。

Output

每行一个数，表示Speakless能赢的概率（用百分比计算，保留到小数点后2位）。

Sample Input

50 50 0.5 0.5
10 10 0.51 0.5
50 50 0.51 0.5

Sample Output

0.50
0.60
0.88

思路：

马尔科夫链（赌徒输光问题）

假设fi 表示Speakless 手上有i 颗糖果、最终赢得比赛的概率。则根据fi 的转移状态有如下公式：

（1）答对获得1 颗糖果变成（i+1）颗糖果，概率为手上有i+1 颗糖果的概率乘以转移概率；

（2）答错失去1 颗糖果变成（i-1）颗糖果；

（3）双方打平，糖果数不变。

接下来做如下运算：

这时为方便运算我们设 则有

因为fi 表示手上有i 颗糖果、最终获得胜利的概率，则有

上述式子两边相加则有

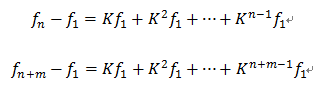
即

（1）等K 不等于1 时

（2）当K 等于1 时

代码：

#include <iostream>
#include <string.h>
#include <math.h>

using namespace std;

const double EPS = 1e-12;

int main()
{
	int n, m;
	double p, q;
	while (scanf("%d%d%lf%lf", &n, &m, &p, &q) != EOF)
	{
		if (n == 0)
		{
			printf("0.00\n");
		}
		else if (m == 0)
		{
			printf("1.00\n");
		}
		else if (p == 0 || q == 1)
		{
			printf("0.00\n");
		}
		else
		{
			double K = (1 - p) * q / p / (1 - q);
			if (fabs(K - 1.0) < EPS)
			{
				printf("%.2lf\n", (double)n / (m + n));
			}
			else
			{
				printf("%.2lf\n", (1 - pow(K, n)) / (1 - pow(K, n + m)));
			}
		}
	}

	system("pause");
	return 0;
}

hdu 1204 糖果大战

标签：

原文地址：http://my.oschina.net/keyven/blog/500982