详解OpenGL中的各种变换（投影变换，模型变换，视图变换）（二）——投影变换

标签：

　　下面介绍投影变换矩阵。这个相比较上一遍的就比较难了。主要分为透视投影矩阵和正交投影矩阵，本文主要介绍透视投影矩阵，正交比较简单，就给出矩阵形式。

　　（1）透视投影变换矩阵

　　我们先来说一下透视投影需要哪些参数。如图1所示，深色部分表示最终显示的区域。照相机的z轴是穿过视锥体正中心的，显示区域离相机最近的平面我们称为Z_near，最远的平面我们称为Z_far。其中Z_near就是最终的投影窗口。所以我们要把Z_near的宽映射到坐标[-1,1]，把Z_near的高映射到坐标[-1,1]，把Z_near到Z_far的深度距离映射到坐标[-1,1]。因为最后的OpenGL绘制的区域其实就是一个从(-1,-1,-1)到(1,1,1)的一个立方体。而且这样映射还有个好处，就是绘制的时候靠近Z_near的对象要比靠近Z_far的对象大。

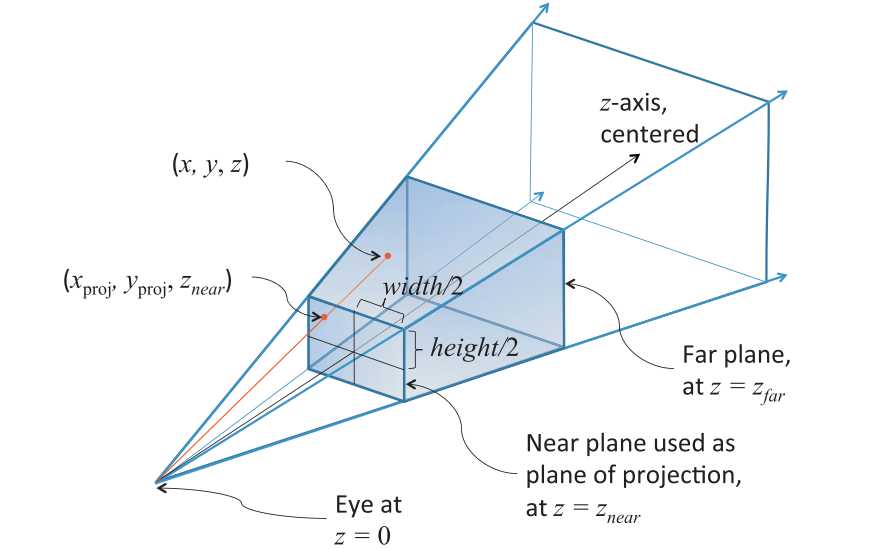
图1

　　根据这些参数我们可以得到投影变换矩阵。首先，对于这个矩阵，我们先来看x轴和y轴。我们结合上图，根据相似三角形可以得到：

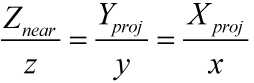
图2

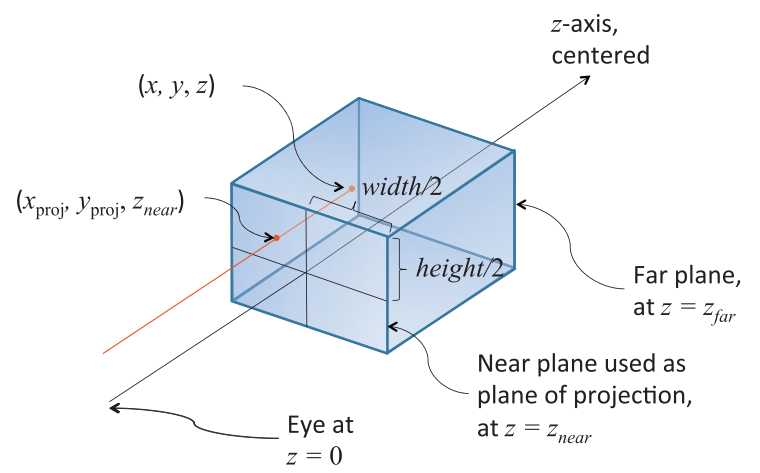
　　我们化简一下可以得到Y_proj=Z_near*x/z和X_proj=Z_near*y/z。之后我们将齐次坐标的w分量设为z，就可以得到Y_proj=Z_near*x和X_proj=Z_near*y。再将坐标映射到[-1,1]，除以投影窗口的长宽即可。我们得到部分透视投影矩阵：

图3

　　我们再来看z轴。其实z轴映射也非常简单。我们假设f(z)=A*z+B，当齐次坐标的w分量为z时，那么实际上z轴的坐标为A+B/z。我们根据映射关系得到下面两个式子：

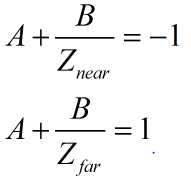
图4

　　再根据这两个式子，求出A和B的值(具体求解就忽略了，得到的结果就是下面矩阵第三行的两个值)。最终得到完整的透视投影变换矩阵：

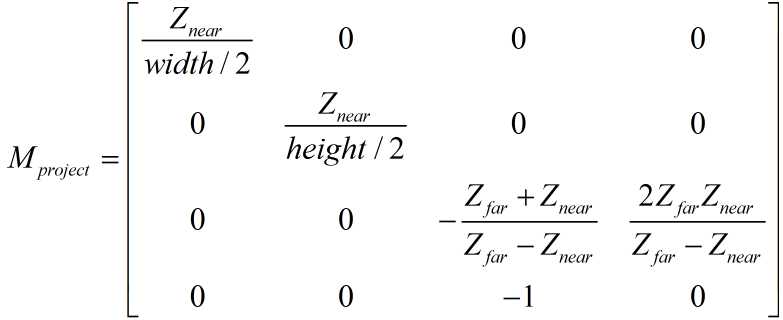
图5

　　我们还可以用另一种方式来表达透视投影。这种方式一共有四个变量。

• 透视的角度fovy。如图6所示，fovy表示的是照相机所看到的范围。
• 投影窗口的宽高比aspect。如图6所示，aspect就是Z_near平面的宽高比。
• 显示区域离相机最近的距离near和离相机最远的距离far。这两个量与前面都是一样的。

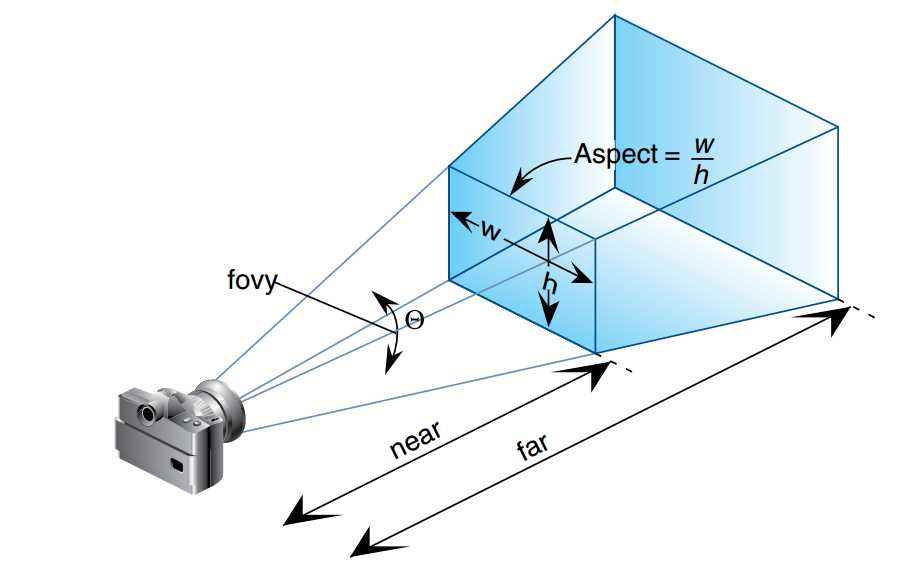
图6

　　这个表达下的透视投影矩阵如下（计算过程跟上面一种基本一致）：

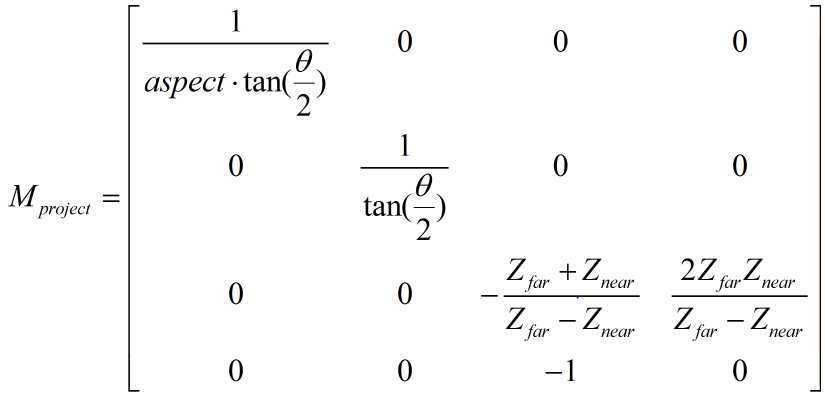
图7

　　（2）正交投影变换矩阵

 　　正交投影就比较简单了。如图8所示，显示区域就是一立方体。因为没有近大远小的特性，齐次坐标的w分量不需要变化，设为1.0就可以了。另外，我们也需要把x轴，y轴，z轴分别映射到坐标[-1,1]。计算过程也和透视投影变化矩阵类似。

详解OpenGL中的各种变换（投影变换，模型变换，视图变换）（二）——投影变换

标签：

原文地址：http://www.cnblogs.com/caster99/p/4783386.html