标签：
上一章节讲解了拓扑排序问题，拓扑排序是解决一个工程能否顺序解决的问题，本质是一个广度层次遍历的过程，通过记录顶点入度问题，进行逐步输出的工作。在实际生活中，往往是求解工程完成需要最短时间问题。比如生活中生产一辆汽车，需要生产各种各样的零件，最终组装成车。例如生产轮子0.5天，发动机3天，底盘2天，其他部件2天，集中全部零件0.5天，组装需要2天。请问组装一辆汽车，最短需要多长时间。根据前面描述，我们构造这样的AOV网络图，一看便知。
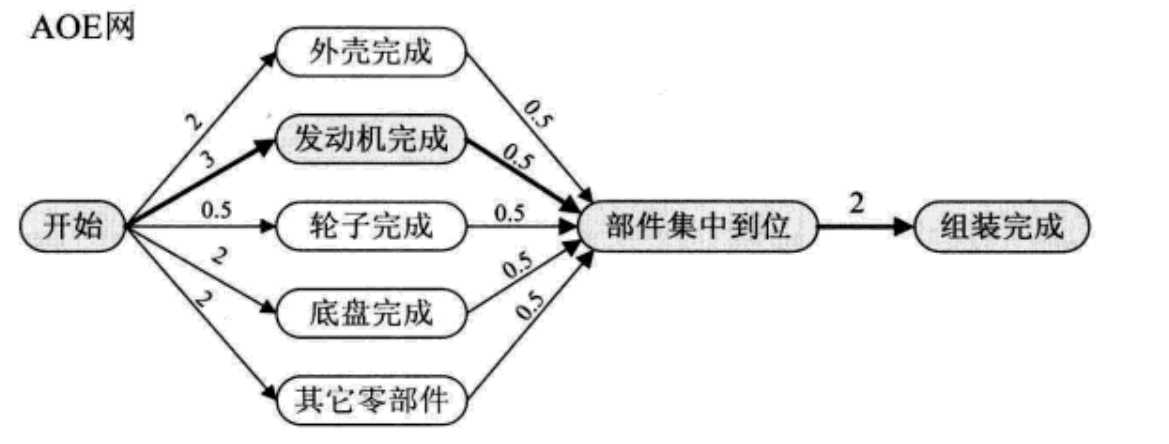
通过网络中，我们很清晰的知道，关键路径是5.5，如果发动机提高效率，那么关键路径就是4.5。对于以项目关键问题就是寻找关键路径，也许对于上图很容易寻找，而对于下图，就需要关键路径算法，进行计算寻找。
关键路径：路径上各个活动所持续的时间之和为路径长度，从源点到汇点具有最大长度的路径叫关键路径。
在介绍关键路径的时，先介绍几个概念
关键路劲算法原理：先获取ve和vl，通过上述两者获取e和l，然后判断e和l是否相等来判断a是否是关键活动。
关键路径算法是一种典型的动态规划法，设图G=(V, E)是个AOE网，结点编号为1,2,...,n，其中结点1与n 分别为始点和终点，ak=<i, j>∈E是G的一个活动。算法关键是确定活动的最早发生时间和最晚发生时间，进而获取顶点的最早开始时间和最晚开始时间。
根据前面给出的定义，可推出活动的最早及最晚发生时间的计算方法：
e(k) = ve(i)
l(k) = vl(j) - len(i,j)
结点的最早发生时间的计算，需按拓扑次序递推：
ve(1) = 0
ve(j) = MAX{ etv(i)+len(i, j) }
对所有<i,j> ∈E的i 结点的最晚发生时间的计算，需按逆拓扑次序递推：
vl(n) = ve(n)
vl(i) = MIN{vl(j) - len(i, j)} 对所有<i,j>∈E的j
这种计算方法， 依赖于拓扑排序， 即计算ve( j) 前，应已求得j 的各前趋结点的ve值，而计算vl(i)前，应已求得i的各后继结点的vl值。ve的计算可在拓扑排序过程中进行，即在每输出一个结点i后，在删除i的每个出边<i,j>（即入度减1）的同时，执行
if ( ve[i]+len(i,j)) > ve[j] )
ve[j] = ve[i] + len(i,j)
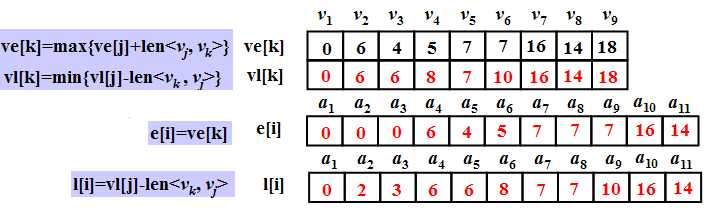所以根据算法：
//改进的拓扑排序，用于关键路径算法 void GraphData::TopoLogicalSortAdv(GraphListAdv *pList) { EdgeNode *e; int ncount = 0; //统计输出顶点个数，用于判断是否有环 int nIndex ; // y用于保存度为0的坐标 stack<int> staNode; for (int i = 0;i < pList->numVertess; i++) { if (pList->vertexList[i].in == 0) { staNode.push(i); //将入度为0的顶点入栈 } } memset(this->veArray,0,pList->numVertess); while(!staNode.empty()) { nIndex = staNode.top(); // 获取入度为0的顶点 staNode.pop(); //出栈 staEtv.push(nIndex); //将弹出的顶点序号压入拓扑序列堆栈 printf("%c ->",pList->vertexList[nIndex].nNodeData); //打印顶点 ncount ++; //对此顶点的处理：下一个顶点入度减1，如果为0还要进栈 for (e = pList->vertexList[nIndex].pFirstNode;e;e = e->next) { //对此顶点弧表遍历 int temp = e->nNodevex; //将temp号顶点邻接点的入度减1,若为0，则入栈，以便于下次循环输出 if (!(--pList->vertexList[temp].in)) { staNode.push(temp); } //求取各个顶点的事件最早发生时间。 if (veArray[nIndex] + e->nNodeWeight > veArray[temp]) { veArray[temp] = veArray[nIndex] + e->nNodeWeight; } } } if (ncount < pList->numVertess) { printf(" 图有内环"); } } //关键路径算法 void GraphData::CriticalPath(GraphListAdv *pList) { EdgeNode *node; int i,j,top,k; int ete,lte; TopoLogicalSortAdv(pList); for (i = 0; i< pList->numVertess;i++) { vlArray[i] = veArray[i]; //初始化vl } while(!staEtv.empty()) { top = staEtv.top(); staEtv.pop(); for (node = pList->vertexList[top].pFirstNode;node;node = node->next) { k = node->nNodevex; if (vlArray[k] - node->nNodeWeight < vlArray[top]) //求取顶点事件的最晚发生时间 { vlArray[top] = vlArray[k] + node->nNodeWeight; } } } //求取关键路径 for (i = 0;i < pList->numVertess;i++) { for (node = pList->vertexList[i].pFirstNode; node;node = node->next) { k = node->nNodevex; ete = veArray[k]; lte = vlArray[k]; if (ete == lte) { printf("<v%c,v%c> length: %d, ",pList->vertexList[i].nNodeData,pList->vertexList[k].nNodeData,node->nNodeWeight); } } } }
程序最后的输出结果如上图。
在程序中首先是利用上一章节的拓扑排序进行改进，包括将顶点入栈，同时获取顶点的最早活动时间，之后根据顶点的最早活动时间，逆序获取顶点最晚活动时间，进而获取项目的最晚活动时间数组。最终结果就如例图解释中所示，获取到每个顶点的最早开始时间和最晚开始时间。
其中最早开始时间和最晚开始时间相等，说明在顶点的活动是没有空闲时间的，关键路径的活动各个顶点就是求取最大路径长度，所以，两者相等就是关键路径的判断条件，算法的关键是利用拓扑排序获取顶点的最早开始时间和最晚开始时间。
1 /* 邻接矩阵表示的图结构*/ 2 #include <stdio.h> 3 #include <stdlib.h> 4 #include <stack> 5 using namespace std; 6 7 8 #define MAXVEX 100 //最大顶点数 9 #define INFINITY 65535 //最大权值 10 11 typedef int EdgeType; //权值类型自己定义 12 typedef char VertexType; //顶点类型自己定义 13 #pragma once 14 15 #pragma region 邻接矩阵结构体 16 typedef struct 17 { 18 VertexType vex[MAXVEX]; //顶点表 19 EdgeType arg[MAXVEX][MAXVEX]; ///权值表-邻接矩阵 20 int numVertexes,numEdges; //图中的边数和顶点数 21 }GraphArray; 22 //边集数组 23 typedef struct 24 { 25 int begin; 26 int end; 27 int weight; 28 }Edge; 29 #pragma endregion 30 31 #pragma region 邻接表结构体 32 //边表结点 33 typedef struct EdgeNode 34 { 35 int nNodevex; //邻接点的点表中结点的坐标 36 EdgeType nNodeWeight; //用于网图中边的权值 37 EdgeNode* next; //链域，指向下一个邻接点 38 }EdgeNode,*pEdgeNode; 39 //顶点表结点 40 typedef struct VertexNode 41 { 42 VertexType nNodeData; //顶点表中存储的数据 43 pEdgeNode pFirstNode; //顶点表和边表中关联指针，指向边表头指针 44 45 }VertexNode,*pVertexNode,VertexList[MAXVEX]; 46 typedef struct VertexNodeAdv 47 { 48 int in; //顶点的度 49 VertexType nNodeData; //顶点表中存储的数据 50 pEdgeNode pFirstNode; //顶点表和边表中关联指针，指向边表头指针 51 }VertexNodeAdv,*pVertexNodeAdv,VertexListAdv[MAXVEX];; 52 //图结构 53 typedef struct 54 { 55 VertexList vertexList; 56 int numVertess,numEdges; 57 }GraphList; 58 59 //图结构 60 typedef struct 61 { 62 VertexListAdv vertexList; 63 int numVertess,numEdges; 64 }GraphListAdv; 65 #pragma endregion 66 67 class GraphData 68 { 69 public: 70 GraphData(void); 71 ~GraphData(void); 72 #pragma region 创建邻接矩阵 73 void CreateGraphArray(GraphArray* pGraphArray,int numVer,int numEdegs); 74 int GetGraphLocation(GraphArray* pGraphArrray,char chpoint); 75 #pragma endregion 76 77 #pragma region 创建邻接表 78 void CreateGraphList(GraphList* pList,int numVer,int numEdegs); 79 void CreateGraphListAdv(GraphListAdv* pList,int numVer,int numEdegs); 80 int GetGraphListLocation(GraphList* pList,char chpoint); 81 int GetGraphAdvListLocation(GraphListAdv* pList,char chpoint); 82 #pragma endregion 83 84 #pragma region 图的遍历 85 //邻接表的深度递归算法 86 void DFS(GraphList *pList,int i); 87 //邻接表的深度遍历操作 88 void DFSTraverse(GraphList* pList); 89 //邻接矩阵的深度递归算法 90 void DFS(GraphArray *pArray,int i); 91 //邻接矩阵的深度遍历操作 92 void DFSTraverse(GraphArray *pArray); 93 //邻接矩阵的广度遍历操作 94 void BFSTraverse(GraphArray *pArray); 95 //邻接表的广度遍历操作 96 void BFSTraverse(GraphList *pList); 97 #pragma endregion 98 99 #pragma region 最小生成树 100 //prime算法 101 void MiniSpanTree_Prime(GraphArray *pArray); 102 //Kruskal算法(克鲁斯卡尔） 103 void MiniSpanTree_Kruskal(GraphArray *pArray); 104 #pragma endregion 105 106 #pragma region 最短路径 107 //Dijkstra算法 108 void ShortPath_Dijkstra(GraphArray *pArray); 109 //Floyd算法 110 void ShortPath_Floyd(GraphArray *pArray); 111 #pragma endregion 112 113 #pragma region 拓扑排序、关键路径 114 //拓扑排序 115 void TopoLogicalSort(GraphListAdv *pList); 116 //改进的拓扑排序，用于关键路径算法 117 void TopoLogicalSortAdv(GraphListAdv *pList); 118 //关键路径算法 119 void CriticalPath(GraphListAdv *pList); 120 #pragma endregion 121 122 private: 123 bool bVisited[MAXVEX]; 124 int veArray[MAXVEX]; 125 int vlArray[MAXVEX]; 126 stack<int> staEtv; 127 128 #pragma region 私有方法 129 130 int FindLastLine(int *parent,int f); 131 132 void InsertSort(Edge *pEdge,int k); 133 134 void GraphToEdges(GraphArray *pArray,Edge *pEdge); 135 #pragma endregion 136 137 };
1 #include "GraphData.h" 2 #include <queue> 3 #include <stack> 4 using namespace std; 5 GraphData::GraphData(void) 6 { 7 } 8 9 10 GraphData::~GraphData(void) 11 { 12 } 13 14 #pragma region 创建邻接矩阵 15 int GraphData::GetGraphLocation(GraphArray* pGraphArrray,char chpoint) 16 { 17 int i = 0; 18 for (i = 0;i< pGraphArrray->numVertexes;i++) 19 { 20 if (pGraphArrray->vex[i] == chpoint) 21 { 22 break;; 23 } 24 } 25 if (i >= pGraphArrray->numVertexes) 26 { 27 return -1; 28 } 29 return i; 30 } 31 /// <summary> 32 /// 创建邻接矩阵 33 /// </summary> 34 void GraphData::CreateGraphArray(GraphArray* pGraphArray,int numVer,int numEdegs) 35 { 36 int weight = 0; 37 pGraphArray->numVertexes = numVer; 38 pGraphArray->numEdges = numEdegs; 39 40 //创建顶点表 41 for (int i= 0; i < numVer;i++) 42 { 43 pGraphArray->vex[i] = getchar(); 44 while(pGraphArray->vex[i] == ‘\n‘) 45 { 46 pGraphArray->vex[i] = getchar(); 47 } 48 } 49 50 //创建邻接表的边矩阵 51 for (int i = 0; i < numEdegs; i++) 52 { 53 for (int j = 0;j < numEdegs ; j++) 54 { 55 pGraphArray->arg[i][j] = INFINITY; 56 } 57 } 58 for(int k = 0; k < pGraphArray->numEdges; k++) 59 { 60 char p, q; 61 printf("输入边(vi,vj)上的下标i，下标j和权值:\n"); 62 63 p = getchar(); 64 while(p == ‘\n‘) 65 { 66 p = getchar(); 67 } 68 q = getchar(); 69 while(q == ‘\n‘) 70 { 71 q = getchar(); 72 } 73 scanf("%d", &weight); 74 75 int m = -1; 76 int n = -1; 77 m = GetGraphLocation(pGraphArray, p); 78 n = GetGraphLocation(pGraphArray, q); 79 if(n == -1 || m == -1) 80 { 81 fprintf(stderr, "there is no this vertex.\n"); 82 return; 83 } 84 //getchar(); 85 pGraphArray->arg[m][n] = weight; 86 pGraphArray->arg[n][m] = weight; //因为是无向图，矩阵对称 87 } 88 89 } 90 91 #pragma endregion 92 93 #pragma region 创建邻接表 94 void GraphData::CreateGraphList(GraphList* pList,int numVer,int numEdegs) 95 { 96 int weight = 0; 97 GraphList *pGraphList = pList; 98 pGraphList->numVertess = numVer; 99 pGraphList->numEdges = numEdegs; 100 EdgeNode* firstNode,*secondNode; 101 //创建顶点表 102 for (int i= 0; i < numVer;i++) 103 { 104 pGraphList->vertexList[i].nNodeData = getchar(); 105 pGraphList->vertexList[i].pFirstNode = NULL; 106 while(pGraphList->vertexList[i].nNodeData == ‘\n‘) 107 { 108 pGraphList->vertexList[i].nNodeData = getchar(); 109 } 110 } 111 112 //创建边表 113 for(int k = 0; k < pGraphList->numEdges; k++) 114 { 115 char p, q; 116 printf("输入边(vi,vj)上的下标i，下标j和权值:\n"); 117 118 p = getchar(); 119 while(p == ‘\n‘) 120 { 121 p = getchar(); 122 } 123 q = getchar(); 124 while(q == ‘\n‘) 125 { 126 q = getchar(); 127 } 128 scanf("%d", &weight); 129 130 int m = -1; 131 int n = -1; 132 m = GetGraphListLocation(pGraphList, p); 133 n = GetGraphListLocation(pGraphList, q); 134 if(n == -1 || m == -1) 135 { 136 fprintf(stderr, "there is no this vertex.\n"); 137 return; 138 } 139 //getchar(); 140 //字符p在顶点表的坐标为m，与坐标n的结点建立联系权重为weight 141 firstNode = new EdgeNode(); 142 firstNode->nNodevex = n; 143 firstNode->next = pGraphList->vertexList[m].pFirstNode; 144 firstNode->nNodeWeight = weight; 145 pGraphList->vertexList[m].pFirstNode = firstNode; 146 147 //第二个字符second 148 secondNode = new EdgeNode(); 149 secondNode->nNodevex = m; 150 secondNode->next = pGraphList->vertexList[n].pFirstNode; 151 secondNode->nNodeWeight = weight; 152 pGraphList->vertexList[n].pFirstNode = secondNode; 153 154 } 155 } 156 157 int GraphData::GetGraphListLocation(GraphList* pList,char chpoint) 158 { 159 GraphList *pGraphList = pList; 160 int i = 0; 161 for (i = 0;i< pGraphList->numVertess;i++) 162 { 163 if (pGraphList->vertexList[i].nNodeData == chpoint) 164 { 165 break;; 166 } 167 } 168 if (i >= pGraphList->numVertess) 169 { 170 return -1; 171 } 172 return i; 173 } 174 175 int GraphData::GetGraphAdvListLocation(GraphListAdv* pList,char chpoint) 176 { 177 GraphListAdv *pGraphList = pList; 178 int i = 0; 179 for (i = 0;i< pGraphList->numVertess;i++) 180 { 181 if (pGraphList->vertexList[i].nNodeData == chpoint) 182 { 183 break;; 184 } 185 } 186 if (i >= pGraphList->numVertess) 187 { 188 return -1; 189 } 190 return i; 191 } 192 #pragma endregion 193 194 #pragma region 图的遍历 195 //邻接表的深度递归算法 196 void GraphData::DFS(GraphList *pList,int i) 197 { 198 EdgeNode *itemNode; 199 bVisited[i] = true; 200 printf("%c",pList->vertexList[i].nNodeData); //打印顶点数据 201 itemNode = pList->vertexList[i].pFirstNode; 202 while(itemNode) 203 { 204 if (!bVisited[itemNode->nNodevex]) 205 { 206 DFS(pList,itemNode->nNodevex); 207 } 208 itemNode = itemNode->next; 209 } 210 } 211 //邻接表的深度遍历操作 212 void GraphData::DFSTraverse(GraphList* pList) 213 { 214 int i; 215 GraphList *pGraphList = pList; 216 for ( i = 0;pGraphList->numVertess;i++) 217 { 218 bVisited[i] = false; 219 } 220 for (i = 0;i < pGraphList->numVertess;i++) 221 { 222 if (!bVisited[i]) 223 { 224 DFS(pGraphList,i); 225 } 226 } 227 } 228 //邻接矩阵的深度递归算法 229 void GraphData::DFS(GraphArray *pArray,int i) 230 { 231 int j = 0; 232 printf("%c",pArray->vex[i]); //打印顶点，也可以其他操作 233 for (j = 0; j< pArray->numVertexes;j++) 234 { 235 if (!bVisited[j]&&pArray->arg[i][j] == 1) //关键之前初始化时，有关系的边赋值为1，所以由此进行判断 236 { 237 DFS(pArray,j); //对为访问的邻接顶点递归调用 238 } 239 } 240 } 241 //邻接矩阵的深度遍历操作 242 void GraphData::DFSTraverse(GraphArray *pArray) 243 { 244 int i; 245 for (i = 0;i < pArray->numVertexes;i++) 246 { 247 bVisited[i] = false; 248 } 249 for(i = 0; i< pArray->numVertexes;i++) 250 { 251 if (!bVisited[i]) 252 { 253 DFS(pArray,i); 254 } 255 } 256 } 257 258 //邻接矩阵的广度遍历操作 259 void GraphData::BFSTraverse(GraphArray *pArray) 260 { 261 queue<int> itemQueue; 262 int i,j; 263 for(i = 0 ;i< pArray->numVertexes;i++) 264 { 265 bVisited[i] = false; 266 } 267 for(i = 0;i< pArray->numVertexes;i++)//每个顶点循环 268 { 269 if (!bVisited[i])//访问未被访问的顶点 270 { 271 bVisited[i] = true; 272 printf("%c",pArray->vex[i]); 273 itemQueue.push(i); //将此结点入队 274 while(!itemQueue.empty()) 275 { 276 int m = itemQueue.front(); //结点出队 277 itemQueue.pop(); 278 for(j = 0;j< pArray->numVertexes;j++) 279 { 280 //判断其他顶点与当前顶点存在边且未被访问过。 281 if (!bVisited[j] && pArray->arg[m][j] == 1) 282 { 283 bVisited[j] = true; 284 printf("%c",pArray->vex[j]); 285 itemQueue.push(j); 286 } 287 } 288 } 289 } 290 } 291 } 292 //邻接表的广度遍历操作 293 void GraphData::BFSTraverse(GraphList *pList) 294 { 295 queue<int> itemQueue; 296 int i,j; 297 EdgeNode* pitemNode; 298 for(i = 0 ;i< pList->numVertess;i++) 299 { 300 bVisited[i] = false; 301 } 302 for(i = 0;i<pList->numVertess;i++) 303 { 304 if (!bVisited[i]) 305 { 306 bVisited[i] = true; 307 printf("%c",pList->vertexList[i].nNodeData); 308 itemQueue.push(i); 309 while(!itemQueue.empty()) 310 { 311 int m = itemQueue.front(); 312 itemQueue.pop(); 313 pitemNode = pList->vertexList[m].pFirstNode; 314 while(pitemNode) 315 { 316 if (bVisited[pitemNode->nNodevex]) 317 { 318 bVisited[pitemNode->nNodevex] = true; 319 printf("%c",pList->vertexList[pitemNode->nNodevex].nNodeData); 320 itemQueue.push(pitemNode->nNodevex); 321 } 322 pitemNode = pitemNode->next; 323 } 324 325 } 326 } 327 } 328 } 329 #pragma endregion 330 331 #pragma region 最小生成树 332 //prime算法 333 void GraphData::MiniSpanTree_Prime(GraphArray *pArray) 334 { 335 int min,i,j,k; 336 int nNodeIndex[MAXVEX]; //保存相关顶点坐标，1就是已经遍历访问的过结点 337 int nNodeWeight[MAXVEX]; //保存某个顶点到各个顶点的权值，为不为0和最大值表示遍历过了。 338 //两个数组的初始化 339 printf("开始初始化，当前顶点边的权值为："); 340 for(i = 0;i<pArray->numVertexes;i++) 341 { 342 nNodeIndex[i] = 0; 343 nNodeWeight[i] = pArray->arg[0][i];//设定在矩阵中第一个顶点为初始点。 344 printf(" %c",nNodeWeight[i]); 345 } 346 nNodeWeight[0] = 0; //选取坐标点0为起始点。 347 //Prime算法思想 348 for (i = 1;i< pArray->numVertexes;i++) 349 { 350 min = INFINITY; //初始化权值为最大值; 351 j = 1; 352 k = 0; 353 // 循环全部顶点，寻找与初始点边权值最小的顶点，记下权值和坐标 354 while(j < pArray->numVertexes) 355 { 356 //如果权值不为0,且权值小于min,为0表示本身 357 if (nNodeWeight[j] != 0&&nNodeWeight[j] < min) 358 { 359 min = nNodeWeight[j]; 360 k = j; //保存上述顶点的坐标值 361 } 362 j++; 363 } 364 printf("当前顶点边中权值最小边(%d,%d)\n",nNodeIndex[k] , k); //打印当前顶点边中权值最小 365 nNodeWeight[k] = 0; //将当前顶点的权值设置为0，表示此顶点已经完成任务 366 367 for (j = 1;j< pArray->numVertexes;j++) //循环所有顶点，查找与k顶点的最小边 368 { 369 //若下标为k的顶点各边权值小于此前这些顶点未被加入的生成树权值 370 if (nNodeWeight[j] != 0&&pArray->arg[k][j] < nNodeWeight[j]) 371 { 372 nNodeWeight[j] = pArray->arg[k][j]; 373 nNodeIndex[j] = k; //将下标为k的顶点存入adjvex 374 } 375 } 376 //打印当前顶点状况 377 printf("坐标点数组为："); 378 for(j = 0;j< pArray->numVertexes;j++) 379 { 380 printf("%3d ",nNodeIndex[j]); 381 } 382 printf("\n"); 383 printf("权重数组为："); 384 for(j = 0;j< pArray->numVertexes;j++) 385 { 386 printf("%3d ",nNodeWeight[j]); 387 } 388 printf("\n"); 389 } 390 391 } 392 //Kruskal算法(克鲁斯卡尔） 393 void GraphData::MiniSpanTree_Kruskal(GraphArray *pArray) 394 { 395 int i,n,m; 396 int parent[MAXVEX]; //定义边集数组 397 Edge edges[MAXVEX]; //定义一数组用来判断边与边是否形成环 398 //邻接矩阵转为边集数组，并按照权值大小排序 399 GraphToEdges(pArray,edges); 400 401 for (i =0; i< pArray->numVertexes;i++) 402 { 403 parent[i] = 0; //初始化数组数值为0 404 405 } 406 407 //算法关键实现 408 for (i = 0;i < pArray->numVertexes;i++) //循环每条边 409 { 410 //根据边集数组，查找出不为0的边 411 n = FindLastLine(parent,edges[i].begin); 412 m = FindLastLine(parent,edges[i].end); 413 printf("边%d的开始序号为：%d，结束为:%d)",i,n,m); 414 if(n != m) //假如n与m不等，说明此边没有与现有生成树形成环路 415 { 416 parent[n] = m; //将此边的结尾顶点放入下标为起点的parent中 417 //表示此顶点已经在生成树集合中 418 printf("(%d,%d) %d ", edges[i].begin, edges[i].end, edges[i].weight); 419 } 420 } 421 printf("\n"); 422 } 423 #pragma endregion 424 425 #pragma region 最短路径 426 //Dijkstra算法 427 void GraphData::ShortPath_Dijkstra(GraphArray *pArray) 428 { 429 //Dijkstra算法和最小生成树的算法，在某种程度是相似的 430 int min,i,j,k; 431 int nNodeIndex[MAXVEX]; //保存相关顶点坐标，1就是已经遍历访问的过结点(在最小生成树中为数值表示遍历过同时值与坐标是一条边） 432 int nNodeWeight[MAXVEX]; //保存某个顶点到各个顶点的权值，为不为0和最大值表示遍历过了。 433 int nPathLength[MAXVEX]; //坐标和元素表示为同时值和坐标表示一边，与Primes有相同的 434 //两个数组的初始化 435 printf("开始初始化，当前顶点边的权值为："); 436 for(i = 0;i<pArray->numVertexes;i++) 437 { 438 nNodeIndex[i] = 0; 439 nNodeWeight[i] = pArray->arg[0][i];//设定在矩阵中第一个顶点为初始点。 440 nPathLength[i] = 0; 441 printf(" %c",nNodeWeight[i]); 442 } 443 nNodeWeight[0] = 0; //选取坐标点0为起始点。 444 nNodeIndex[0] = 1; //这样0就是起始点，设为1.（和Prime的不同） 445 //算法思想 446 for (i = 1;i< pArray->numVertexes;i++) 447 { 448 min = INFINITY; //初始化权值为最大值; 449 j = 1; 450 k = 0; 451 // 循环全部顶点，寻找与初始点边权值最小的顶点，记下权值和坐标 452 while(j < pArray->numVertexes) 453 { 454 //如果权值不为0,且权值小于min,为0表示本身 455 if (!nNodeIndex[j]&&nNodeWeight[j] < min) //这里Prime是权重中不为0, 456 { 457 min = nNodeWeight[j]; 458 k = j; //保存上述顶点的坐标值 459 } 460 j++; 461 } 462 printf("当前顶点边中权值最小边(%d,%d)\n",nNodeIndex[k] , k); //打印当前顶点边中权值最小 463 //nNodeWeight[k] = 0; //将当前顶点的权值设置为0，表示此顶点已经完成任务 464 nNodeIndex[k] = 1; //将目前找到的最近的顶点置为1 465 466 //for (j = 1;j< pArray->numVertexes;j++) //循环所有顶点，查找与k顶点的最小边 467 //{ 468 // //若下标为k的顶点各边权值小于此前这些顶点未被加入的生成树权值 469 // if (nNodeWeight[j] != 0&&pArray->arg[k][j] < nNodeWeight[j]) 470 // { 471 // nNodeWeight[j] = pArray->arg[k][j]; 472 // nNodeIndex[j] = k; //将下标为k的顶点存入adjvex 473 // } 474 //} 475 //修正当前最短路径及距离 476 for (j = 1;j< pArray->numVertexes;j++) //循环所有顶点，查找与k顶点的最小边 477 { 478 //若下标为k的顶点各边权值小于此前这些顶点未被加入的生成树权值 479 if (!nNodeIndex[j] && pArray->arg[k][j] + min< nNodeWeight[j]) 480 { 481 nNodeWeight[j] = pArray->arg[k][j] + min; 482 nPathLength[j] = k; //将下标为k的顶点存入adjvex 483 } 484 } 485 //打印当前顶点状况 486 printf("坐标点数组为："); 487 for(j = 0;j< pArray->numVertexes;j++) 488 { 489 printf("%3d ",nPathLength[j]); 490 } 491 printf("\n"); 492 printf("权重数组为："); 493 for(j = 0;j< pArray->numVertexes;j++) 494 { 495 printf("%3d ",nNodeWeight[j]); 496 } 497 printf("\n"); 498 } 499 500 } 501 //Floyd算法 502 void GraphData::ShortPath_Floyd(GraphArray *pArray) 503 { 504 int i,j,m,k; 505 int nNodeIndex[MAXVEX][MAXVEX]; 506 int nNodeWeight[MAXVEX][MAXVEX]; 507 508 for ( i = 0;i< pArray->numVertexes;i++) 509 { 510 for (j = 0;j< pArray->numVertexes;j++) 511 { 512 nNodeIndex[i][j] = j; /* 初始化 */ 513 nNodeWeight[i][j] = pArray->arg[i][j]; /* [i][j]值即为对应点间的权值 */ 514 } 515 } 516 for (i = 0;i< pArray->numVertexes;i++) 517 { 518 for (j = 0;j< pArray->numVertexes;j++) 519 { 520 for (k = 0;k<pArray->numVertexes;k++) 521 { 522 if (pArray->arg[j][k] > pArray->arg[j][i] + pArray->arg[i][k]) 523 { 524 /* 如果经过下标为k顶点路径比原两点间路径更短 */ 525 nNodeWeight[j][k] = pArray->arg[j][i] + pArray->arg[i][k]; /* 将当前两点间权值设为更小的一个 */ 526 nNodeIndex[j][k] = nNodeIndex[j][i]; /* 路径设置为经过下标为k的顶点 */ 527 } 528 } 529 } 530 } 531 for (i = 0; i< pArray->numVertexes;i++) 532 { 533 for (j = 0;j< pArray->numVertexes;j++) 534 { 535 printf("v%d-v%d weight: %d",i,j,nNodeWeight[i][j]); 536 m = nNodeIndex[i][j]; //获得第一个路径点的顶点下标 537 printf("path :%d",i); //打印源点 538 while(m!=j) 539 { 540 printf(" -> %d",m); //打印路径顶点 541 m = nNodeIndex[m][j]; //获取下一个路径顶点下标 542 } 543 printf(" -> %d\n",m); //打印路径终点。 544 } 545 546 printf("\n"); 547 } 548 } 549 #pragma endregion 550 551 #pragma region 拓扑排序、关键路径 552 void GraphData::CreateGraphListAdv(GraphListAdv* pList,int numVer,int numEdegs) 553 { 554 int weight = 0; 555 GraphListAdv *pGraphList = pList; 556 pGraphList->numVertess = numVer; 557 pGraphList->numEdges = numEdegs; 558 EdgeNode* firstNode,*secondNode; 559 //创建顶点表 560 for (int i= 0; i < numVer;i++) 561 { 562 pGraphList->vertexList[i].nNodeData = getchar(); 563 pGraphList->vertexList[i].pFirstNode = NULL; 564 while(pGraphList->vertexList[i].nNodeData == ‘\n‘) 565 { 566 pGraphList->vertexList[i].nNodeData = getchar(); 567 } 568 } 569 570 //创建边表 571 for(int k = 0; k < pGraphList->numEdges; k++) 572 { 573 char p, q; 574 printf("输入边(vi,vj)上的下标i，下标j和权值:\n"); 575 576 p = getchar(); 577 while(p == ‘\n‘) 578 { 579 p = getchar(); 580 } 581 q = getchar(); 582 while(q == ‘\n‘) 583 { 584 q = getchar(); 585 } 586 scanf("%d", &weight); 587 588 int m = -1; 589 int n = -1; 590 m = GetGraphAdvListLocation(pGraphList, p); 591 n = GetGraphAdvListLocation(pGraphList, q); 592 if(n == -1 || m == -1) 593 { 594 fprintf(stderr, "there is no this vertex.\n"); 595 return; 596 } 597 //getchar(); 598 //字符p在顶点表的坐标为m，与坐标n的结点建立联系权重为weight 599 firstNode = new EdgeNode(); 600 firstNode->nNodevex = n; 601 firstNode->next = pGraphList->vertexList[m].pFirstNode; 602 pGraphList->vertexList[n].in++; 603 firstNode->nNodeWeight = weight; 604 pGraphList->vertexList[m].pFirstNode = firstNode; 605 606 ////第二个字符second 607 //secondNode = new EdgeNode(); 608 //secondNode->nNodevex = m; 609 //secondNode->next = pGraphList->vertexList[n].pFirstNode; 610 //pGraphList->vertexList[n].in++; 611 //secondNode->nNodeWeight = weight; 612 //pGraphList->vertexList[n].pFirstNode = secondNode; 613 614 } 615 } 616 void GraphData::TopoLogicalSort(GraphListAdv *pList) 617 { 618 EdgeNode *e; 619 int ncount = 0; //统计输出顶点个数，用于判断是否有环 620 int nIndex ; // y用于保存度为0的坐标 621 stack<int> staNode; 622 for (int i = 0;i < pList->numVertess; i++) 623 { 624 if (pList->vertexList[i].in == 0) 625 { 626 staNode.push(i); //将入度为0的顶点入栈 627 } 628 } 629 while(!staNode.empty()) 630 { 631 nIndex = staNode.top(); // 获取入度为0的顶点 632 staNode.pop(); //出栈 633 printf("%c ->",pList->vertexList[nIndex].nNodeData); //打印顶点 634 ncount ++; 635 //对此顶点的处理：下一个顶点入度减1，如果为0还要进栈 636 for (e = pList->vertexList[nIndex].pFirstNode;e;e = e->next) 637 { 638 //对此顶点弧表遍历 639 int temp = e->nNodevex; 640 //将temp号顶点邻接点的入度减1,若为0，则入栈，以便于下次循环输出 641 if (!(--pList->vertexList[temp].in)) 642 { 643 staNode.push(temp); 644 } 645 } 646 } 647 if (ncount < pList->numVertess) 648 { 649 printf(" 图有内环"); 650 } 651 652 } 653 //改进的拓扑排序，用于关键路径算法 654 void GraphData::TopoLogicalSortAdv(GraphListAdv *pList) 655 { 656 EdgeNode *e; 657 int ncount = 0; //统计输出顶点个数，用于判断是否有环 658 int nIndex ; // y用于保存度为0的坐标 659 stack<int> staNode; 660 661 for (int i = 0;i < pList->numVertess; i++) 662 { 663 if (pList->vertexList[i].in == 0) 664 { 665 staNode.push(i); //将入度为0的顶点入栈 666 } 667 } 668 memset(this->veArray,0,pList->numVertess); 669 670 while(!staNode.empty()) 671 { 672 nIndex = staNode.top(); // 获取入度为0的顶点 673 staNode.pop(); //出栈 674 staEtv.push(nIndex); //将弹出的顶点序号压入拓扑序列堆栈 675 printf("%c ->",pList->vertexList[nIndex].nNodeData); //打印顶点 676 ncount ++; 677 //对此顶点的处理：下一个顶点入度减1，如果为0还要进栈 678 for (e = pList->vertexList[nIndex].pFirstNode;e;e = e->next) 679 { 680 //对此顶点弧表遍历 681 int temp = e->nNodevex; 682 //将temp号顶点邻接点的入度减1,若为0，则入栈，以便于下次循环输出 683 if (!(--pList->vertexList[temp].in)) 684 { 685 staNode.push(temp); 686 } 687 //求取各个顶点的事件最早发生时间。 688 if (veArray[nIndex] + e->nNodeWeight > veArray[temp]) 689 { 690 veArray[temp] = veArray[nIndex] + e->nNodeWeight; 691 } 692 } 693 } 694 if (ncount < pList->numVertess) 695 { 696 printf(" 图有内环"); 697 } 698 } 699 //关键路径算法 700 void GraphData::CriticalPath(GraphListAdv *pList) 701 { 702 EdgeNode *node; 703 int i,j,top,k; 704 int ete,lte; 705 TopoLogicalSortAdv(pList); 706 for (i = 0; i< pList->numVertess;i++) 707 { 708 vlArray[i] = veArray[i]; //初始化vl 709 } 710 711 while(!staEtv.empty()) 712 { 713 top = staEtv.top(); 714 staEtv.pop(); 715 for (node = pList->vertexList[top].pFirstNode;node;node = node->next) 716 { 717 k = node->nNodevex; 718 if (vlArray[k] - node->nNodeWeight < vlArray[top]) //求取顶点事件的最晚发生时间 719 { 720 vlArray[top] = vlArray[k] + node->nNodeWeight; 721 } 722 723 } 724 725 } 726 //求取关键路径 727 for (i = 0;i < pList->numVertess;i++) 728 { 729 for (node = pList->vertexList[i].pFirstNode; node;node = node->next) 730 { 731 k = node->nNodevex; 732 ete = veArray[k]; 733 lte = vlArray[k]; 734 if (ete == lte) 735 { 736 printf("<v%c,v%c> length: %d, ",pList->vertexList[i].nNodeData,pList->vertexList[k].nNodeData,node->nNodeWeight); 737 } 738 } 739 } 740 741 } 742 #pragma endregion 743 #pragma region 私有方法 744 745 //查找连线顶点尾部 746 int GraphData::FindLastLine(int *parent,int f) 747 { 748 while(parent[f] >0) 749 { 750 f = parent[f]; 751 } 752 return f; 753 } 754 //直接插入排序 755 void GraphData::InsertSort(Edge *pEdge,int k) 756 { 757 Edge *itemEdge = pEdge; 758 Edge item; 759 int i,j; 760 for (i = 1;i<k;i++) 761 { 762 if (itemEdge[i].weight < itemEdge[i-1].weight) 763 { 764 item = itemEdge[i]; 765 for (j = i -1; itemEdge[j].weight > item.weight ;j--) 766 { 767 itemEdge[j+1] = itemEdge[j]; 768 } 769 itemEdge[j+1] = item; 770 } 771 } 772 } 773 //将邻接矩阵转化为边集数组 774 void GraphData::GraphToEdges(GraphArray *pArray,Edge *pEdge) 775 { 776 int i; 777 int j; 778 int k; 779 780 k = 0; 781 for(i = 0; i < pArray->numVertexes; i++) 782 { 783 for(j = i; j < pArray->numEdges; j++) 784 { 785 if(pArray->arg[i][j] < 65535) 786 { 787 pEdge[k].begin = i; 788 pEdge[k].end = j; 789 pEdge[k].weight = pArray->arg[i][j]; 790 k++; 791 } 792 } 793 } 794 795 printf("k = %d\n", k); 796 printf("边集数组排序前，如下所示.\n"); 797 printf("edges[] beign end weight\n"); 798 for(i = 0; i < k; i++) 799 { 800 printf("%d", i); 801 printf(" %d", pEdge[i].begin); 802 printf(" %d", pEdge[i].end); 803 printf(" %d", pEdge[i].weight); 804 printf("\n"); 805 } 806 807 808 //下面进行排序 809 InsertSort(pEdge, k); 810 811 printf("边集数组排序后，如下所示.\n"); 812 printf("edges[] beign end weight\n"); 813 for(i = 0; i < k; i++) 814 { 815 printf("%d", i); 816 printf(" %d", pEdge[i].begin); 817 printf(" %d", pEdge[i].end); 818 printf(" %d", pEdge[i].weight); 819 printf("\n"); 820 } 821 822 } 823 #pragma endregion
1 #include <iostream> 2 #include "GraphData.h" 3 using namespace std; 4 // 5 6 void PrintGrgph(GraphList *pGraphList) 7 { 8 int i =0; 9 while(pGraphList->vertexList[i].pFirstNode != NULL && i<MAXVEX) 10 { 11 printf("顶点:%c ",pGraphList->vertexList[i].nNodeData); 12 EdgeNode *e = NULL; 13 e = pGraphList->vertexList[i].pFirstNode; 14 while(e != NULL) 15 { 16 printf("%d ", e->nNodevex); 17 e = e->next; 18 } 19 i++; 20 printf("\n"); 21 } 22 23 } 24 int main() 25 { 26 int numVexs,numEdges; 27 GraphData* pTestGraph = new GraphData(); 28 GraphArray graphArray; 29 GraphArray* pGraphArray = &graphArray; 30 GraphList* pGgraphList = new GraphList(); 31 GraphListAdv *pGraphListAdv = new GraphListAdv(); 32 33 cout<<"输入顶点数和边数"<<endl; 34 cin>>numVexs>>numEdges; 35 cout<<"顶点数和边数为："<<numVexs<<numEdges<<endl; 36 pTestGraph->CreateGraphListAdv(pGraphListAdv,numVexs,numEdges); 37 //pTestGraph->CreateGraphArray(pGraphArray,numVexs,numEdges); 38 //pTestGraph->MiniSpanTree_Prime(pGraphArray); 39 printf("构建的邻接矩阵如下所示.\n"); 40 /*for(int i = 0; i< numEdges;i++) 41 { 42 for (int j = 0;j< numEdges;j++) 43 { 44 printf("%5d ", pGraphArray->arg[i][j]); 45 } 46 cout<<endl; 47 }*/ 48 //pTestGraph->MiniSpanTree_Kruskal(pGraphArray); 49 /*pTestGraph->CreateGraphList(pGgraphList,numVexs,numEdges); 50 PrintGrgph(pGgraphList);*/ 51 //pTestGraph->ShortPath_Dijkstra(pGraphArray); 52 //pTestGraph->ShortPath_Floyd(pGraphArray); 53 pTestGraph->CriticalPath(pGraphListAdv); 54 system("pause"); 55 }
标签：
原文地址：http://www.cnblogs.com/polly333/p/4786692.html
