标签:
题目一:有这么一个表格,开始的位置在最左下角,一次只能向右或者向上跳一步,问从左下角到右上角一共有多少种走法?

不妨先从第一步开始分析,根据题意 每一步只能往上或者往下,那往上走一步试试。
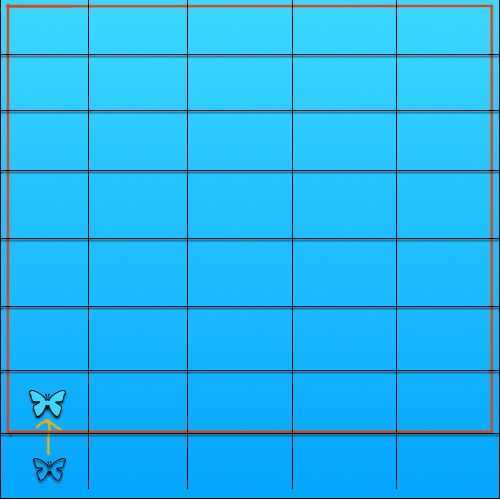
会发现现在只有红色区域可以行动了,只看红色区域会发现,又是一样的问题,只是行数少了一个。同理,向右只是列数少了一个。
如果把一个八行五列的表格总共的步数表示为 f(8,5),那么显然 f(8,5)=f(7,5)+f(8,4)
同时最后一定是f(1,1)=0
那么写出递归解法
1 def find_n_steps(row, col): 2 if row == 1 and col == row: 3 return 0 4 result = 0 5 if row > 1: 6 result += 1 + find_n_steps(row - 1, col) 7 if col > 1: 8 result += 1 + find_n_steps(row, col - 1) 9 return result
然而里面有存在重复的计算, 比如f(7,5)和f(8,4)都会算一个f(7,4)
题目二: 青蛙跳台阶,一次只能跳一次或两次,问上n层有多少种跳法?
由第一题一样的思路,得出 f(n)=f(n-1)+f(n-2) 。同时会发现这是一个斐波那契数列。
def find_n_steps(n):
if n < 1:
return Exception("Invalid input")
return __find_n_steps(n)
def __find_n_steps(n):
if n == 1:
return 1
if n == 2:
return 1
return find_n_steps(n - 1) + find_n_steps(n - 2)
但是呢, 像第一题一样,里面会出现很多重复计算 比如f(n-1)里面又包括了f(n-2)的结果,所以可以换种循环的方式
def fibonacci(n):
if n < 1:
return Exception("Invalid input")
if n == 1:
return 1
if n == 2:
return 1
count = 2
sub1 = 1
sub2 = 1
current = -1
while count < n:
current = sub1 + sub2
sub2 = sub1
sub1 = current
count += 1
return current
标签:
原文地址:http://www.cnblogs.com/imyijie/p/4787022.html