标签:
【题目】LeetCode(5): Longest Palindromic Substring
URL: https://leetcode.com/problems/longest-palindromic-substring/
【描述】
Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.
Input: abceabcdadbcafdavadcadedcvadcd
Output: davad
【中文描述】给一个String,要求返回其中最长的回文子串。题目明确串最长1000个字符,同时有且仅有一个最长回文串。
————————————————————————————————————————————————————————————
【初始思路】
Brute解法谁都能给出来,所以我压根就没动手写,而且明显是O(n3)的时间复杂度。太慢了。
于是换个思路解决,我们从回文串的特点出发看看有没有什么线索。
【回文串/Palindromic】
回文串意指字符串有一个中间点,在中间点的左边和右边的串是镜像相同的,例如:‘davad’,或者‘abccba’。对于前者,‘v’就是中间点。对于后者,可以抽象地认为cc中间有一个中间点。
【解题思路】
由于回文串中间点两边的某一个长度内的与中间点(center)距离(半径)相同的字符一定相同。那么,我们可以考虑不断推移中间点(center),然后对每个中间点,给两个指针(p1,p2)指向其左右字符,只要相同,指针左右各推一位(p1--, p2++。回文串直径不断expand),直到遇到不相同的则停止,然后比较本次得到的回文串直径和现有最大直径的大小,如果本次大则更新最大直径为本次直径。中间点继续后移,重复以上工作。直到遍历完整个String。具体可看下面图帮助理解:
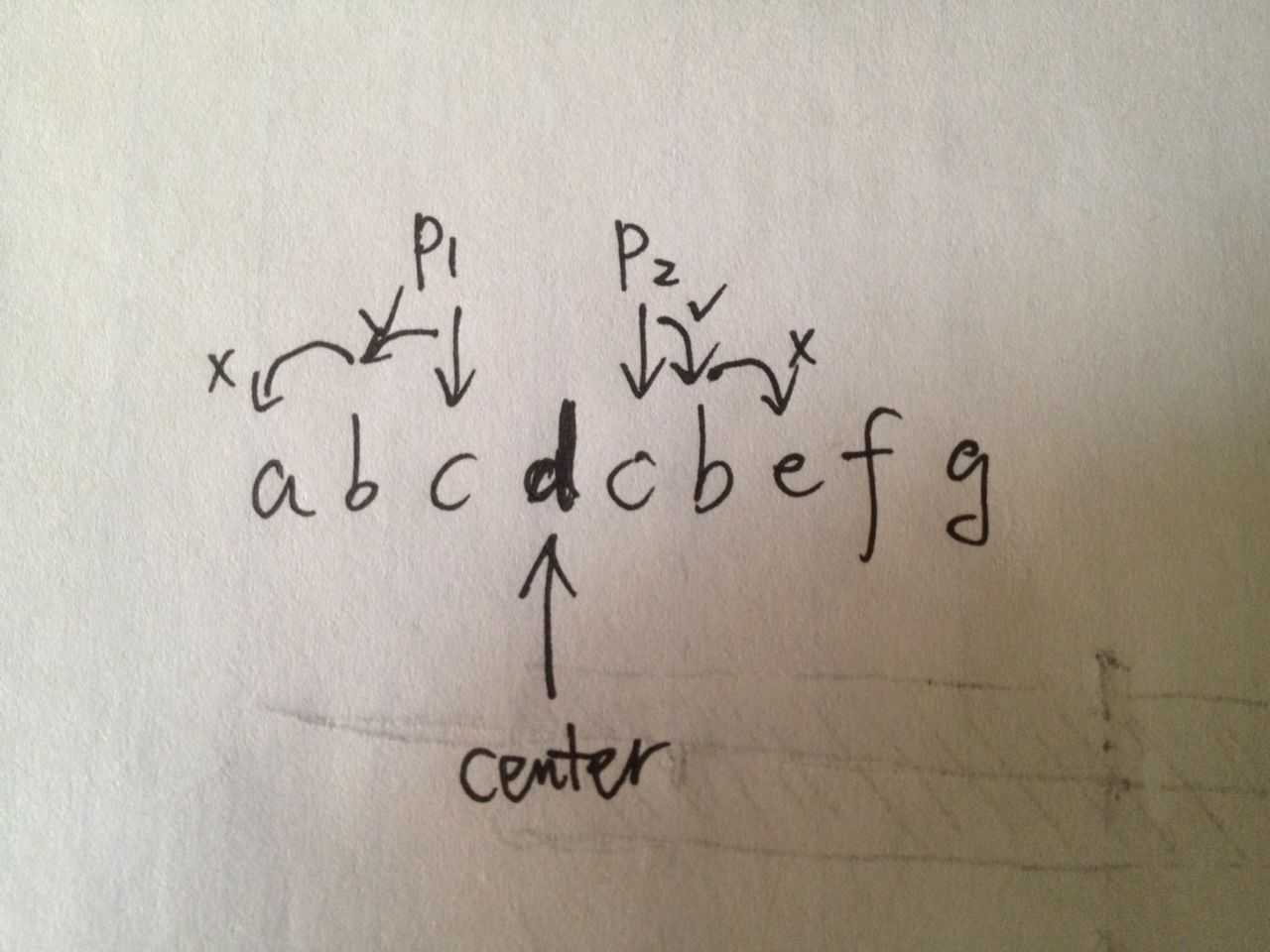
字丑了点,不过理解是足够了,center在‘d‘,p1指向左c,p2指向右c。arr[p1]==arr[p2],所以thislen++,并且p1--, p2++。知道p1指向a,而p2指向了e。推移结束。thislen==5。也即,以d为中心的回文串最长长度为5。下一步,center将推移到右c,然后重复上面过程。
很简单吧?
【问题分析】
以上方法应该可行,但是有一些潜在的问题我们没有考虑进去:
(1)对于abba这种情况,中间点如何找?
(2)推移后,回文串的直径距离如何更新?如何重算?
(3)如何返回?
(4)对string直接做操作?
对于问题(1),我们假设现在中间点(center)在第一个b的位置, 在左右计算完半径后,应当后移。如果直接后移,那么abba这个串肯定找不到了。因为实际的中间点在bb中间。所以对于每一个中间点,对其单独判断完半径后,还需要看看当前中间点字符是否与后一个字符相同,如果相同,我们应当认为中间点后移了0.5个位置。在实际处理的过程中,实际是把左指针指向当前点,同时把右指针指向下一个相同字符再算一次半径。算完后再推移,问题可解决。
对于问题(2),其实考虑清楚。对于中间点就是某个字符的情况,距离从1开始加(因为这个字符就算一个长度为1的回文串);对于中间点在两个相同字符中间的情况,距离初始即为2。 左右指针每推移一位,距离+1,直到左右指针所指字符不再相等。
对于问题(3),我们一定要看清题意。题目要求返回的是一个子串,而不是长度。也即,每当我们更新最大回文串长度的时候,需要把回文串首位位置记录下来。最后在return的时候,按照这个位置找substring即可。同时应当注意String.substring(int start, int end)的用法。
对于问题(4),答案是否定的。对String直接做操作,取其中每一位都只能使用charAt或者substring这些操作,代码实现会比较麻烦。substring更糟糕,它实际返回了一个new String object。对性能会造成巨大影响。所以,我们的第一步,就是s.toCharArray(),后面对这个char[]做操作即可。每一次读取都是O(1)时间,并且对数组做操作是我们最擅长的嘛。
Ok, 分析的差不多了, let‘s code!
【Show me the Code!!!】

1 public static String longestPalindrome(String s) { 2 char[] ss = s.toCharArray(); 3 int current = 0; 4 int p1=0, p2=0; 5 int maxlen = 0; 6 int thislen = 1; 7 int[] pos = new int[2]; 8 while(current<ss.length-1 || (ss.length-1-current)>maxlen/2 ) { 9 p1 = current - 1; 10 p2 = current + 1; 11 thislen = 1; 12 while(p1>=0 && p2<=ss.length-1) { 13 if(ss[p1] == ss[p2]) { 14 thislen += 2; 15 if(maxlen<thislen) { 16 //update the pos 17 maxlen = thislen; 18 pos[0] = p1; 19 pos[1] = p2; 20 } 21 p1--; 22 p2++; 23 } else { 24 break; 25 } 26 } 27 if(ss[current] == ss[current+1]){ 28 p1 = current; 29 p2 = current + 1; 30 thislen = 0; 31 while(p1>=0 && p2<=ss.length-1) { 32 if(ss[p1] == ss[p2]) { 33 thislen += 2; 34 if(maxlen<thislen) { 35 //update the pos 36 maxlen = thislen; 37 pos[0] = p1; 38 pos[1] = p2; 39 } 40 p1--; 41 p2++; 42 } else { 43 break; 44 } 45 } 46 current++; 47 } else { 48 current++; 49 } 50 } 51 52 return s.substring(pos[0], pos[1]+1); 53 }
【反思】
上面解法长是长了点,但是代码清晰易读(当然可以把中间扩展半径的部分用另外一个函数写,我认为代码好坏不是长短来衡量的。好代码的第一标准应该是易读。不要多度优化,记住Knuth说过,过早优化是万恶之源["Premature optimization is the root of all evil (or at least most of it) in programming"]),同时我们实际上还在current后移到一定程度的时候将其与最大maxlen/2做了比较,如果最后还剩余的长度已经不及maxlen的一半,那就根本没必要再推移下去。因为即使全部推移到结束,所得也至多和maxlen一样长(实际根据题意,一样长是不可能的),所以在current达到这样的点的时候可以直接循环结束,减少无谓。
However,这个算法还是略慢(O(n2)),空间O(n)。有没有可能缩减到O(n)时间呢?
思考了一个下午,无所得,最后只能翻看LeetCode的discuss,然后找到这篇(http://articles.leetcode.com/2011/11/longest-palindromic-substring-part-ii.html)。介绍了超级牛逼的Manacher‘s Algorithm:
它可以在O(n)时间内kill掉这个题。英文好的同学可以直接看原文或者Manacher大神的paper。我用了一个晚上认真研读这篇文章,并且用手推演了一遍manacher算法,最后才算搞懂了一二。我这里用中文根据自己的理解写一下,一是加深自己的理解,二是帮助更多同学理解这个牛逼算法。
我们再考虑下回文串的特性,考虑如下串:
a d e b c d e d c b a c a d
这里有一个回文串,bcdedcb,其长度为7。显然,e是其center,其半径radius为7/2 = 3。那么在其半径范围内的字符,假设其下标为i,并且i>center(右半径内)。那么可以轻易看出,其镜像位置为(center-(i-center))i‘ , i与i‘的值必然相等(i-center==3时,b==b; i-center==2时,c==c; i-center ==1时, d==d)。
于是,我们得到回文串定理1:
定理1:给定回文串p,其中心为center,其回文半径为r。对于回文串右半径内的位置i,其值p[i]一定等于其镜像位置值p[i‘](镜像位置i‘ = center-(i-center))。对于左半径内的i,其镜像位置i‘ = center + (center-i)。
继续探索, 考虑如下串:
i‘ c i
b a b a b c d e d c b a b a d
最大回文串用下划线标出。center为e,半径radius为len/2 = 13/2 = 6。 假设现在 i 和其镜像位置 i‘ 已经标出,由定理1,显然其值都是‘a‘。
如果我们现在需要考虑以这两个位置为center的回文长度,它们各自的回文半径是多少呢?对于 i‘ 其半径可以算出为1,其回文串长度为3(如红色字符标出)。 那么由 i‘ 的回文长度是否可以不用计算直接得到 i 的回文长度?答案是肯定的。 由定理1可知,对于目前的 i 和 i‘来说,i 的回文长度 == i‘ 的回文长度 == 3。可以不用计算,直接得到这个值。
但是这个结论不是通用的,还是上面的串,当 i++并且i‘--后,此结论就不一定了:
i‘ c i
b a b a b c d e d c b a b a d
显然,i‘ 为center的回文串长度为5,半径为2。 而 i 为center的回文串长度只有3,半径只有1。哪里出了问题?可以很清楚地看到,由于 i 所处的位置被 center=e的回文串右半径覆盖的长度只有1,如果再右移就说不准是否和其镜像位置 i‘ 再往左移2位相同了(上例中,‘d‘!=‘b‘)。所以,对于这种情况,i 的半径不再等同于 i‘ 的半径,而只能等于(R - i)。
到了这一步,我们的考虑就比较全面了。如果我们能够从左往右一次遍历实时计算得到以每个字符为center对应的半径数据,在遍历结束后,从这些数据中找到最大的那个数,不就是最长回文串的半径吗?没错,这就是Manacer算法!
当然,我们需要对字符串做一点点小的改动,以使得我们计算出的数值就是回文串的长度而不是其半径,这样更不容易出错,也更好编码。
还是上面的串,我们在每个字符间插入字符"#",并且首尾加上防越界字符,看看结果:
i‘ c i
# b # a # b # a # b # c # d # e # d # c # b # a # b # a # d # $
此时得到的串,我们命名为T串。我们将每个字符对应的以其为中心的回文串长度也记录在一个数组中,该数组命名为P[]。显然每个 P[i] 代表了以 T[i] 为中心的回文串的长度。为什么?因为我们加入了#,使得每个原始字符串中的字符间距从1变为了2。现在我们计算的半径,就等同于原始字符串中的回文长度了,举个例子:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
# b # a # b # a # b # c # d # e # d # c # b # a # b # a # d # $。
在e的位置center=15,其P[15] = 13。此时算的是半径,换算成未加#之前的原始字符串,13就是以e为中心的回文串的长度。所以,做这个小小加工的目的,仅仅是为了编码更加方便,并且可以自动转换为原始串的回文长度,这个想法精妙吧?不由得给Manacher大神跪一个!
好了,下一步,看看总体核心算法:
首先,需要的变量先准备好:
int center = 0; //初始中心点,后面会不断更新它;
int R = 0; //初始半径, 后面会不断更新它;
char[] T = new char[N+several#]; // T预处理后的串
int[] P = new int[T.length]; //记录半径的数组,最后结果将基于其中的最大值
显然,需要有一个遍历的过程,所以算法主体将是一个for:
for (int i =1; i<T.length-1; i++) {...} //从1开始是因为从0开始无法向左扩展,所以直接从1开始。
核心算法在于如何计算、更新P[i],根据以上分析,这里给出伪码:
if P[ i’ ] ≤ R – i,
P[ i ] ← P[ i’ ]
else P[ i ] = R - i. // 根据上面分析,如果P[i‘] > R-i,显然如果P[i] = P[i‘],那其右半径很有可能超出了center对应的R。这是危险的,因为那个位置还没有探测到。
好了,最后一步是确定如何更新center和R,其实很简单:只有当目前算出的 i + P[i] > R时,需要更新center和R:
if (i + P[i] > R) {
随着i不断推移,我们必将得到一个数组P,存储了各个 i 位置为中心的各个回文串的长度,从中读出最大的一个,其 i 就是这个回文串的center,然后其长度为P[i],其左起位置为 i - P[i] - 1(对应到原串还需除以2)。substring易求。
【Show me the Code!!!】

1 // Transform S into T. 2 // For example, S = "abba", T = "^#a#b#b#a#$". 3 // ^ and $ signs are sentinels appended to each end to avoid bounds checking 4 public static String preProcess(String s) { 5 int n = s.length(); 6 if (n == 0) return "^$"; 7 StringBuffer ret = new StringBuffer("^"); // starter, meaningless 8 for (int i = 0; i < n; i++) 9 ret.append("#").append(s.substring(i, 1)); 10 11 ret.append("#$"); 12 return ret.toString(); 13 } 14 15 public static String longestPalindrome(String s) { 16 char[] T = preProcess(s).toCharArray(); 17 int n = T.length; 18 int[] P = new int[n]; 19 int C = 0, R = 0; //C stands for center, R stands for radius 20 for (int i = 1; i < n-1; i++) { 21 int i_mirror = 2*C-i; // equals to i‘ = C - (i-C) 22 23 P[i] = (R > i) ? min(R-i, P[i_mirror]) : 0; 24 25 // Attempt to expand palindrome centered at i 26 while (T[i + 1 + P[i]] == T[i - 1 - P[i]]) 27 P[i]++; 28 29 // If palindrome centered at i expand past R, 30 // adjust center based on expanded palindrome. 31 if (i + P[i] > R) { 32 C = i; 33 R = i + P[i]; 34 } 35 } 36 37 // Find the maximum element in P. 38 int maxLen = 0; 39 int centerIndex = 0; 40 for (int i = 1; i < n-1; i++) { 41 if (P[i] > maxLen) { 42 maxLen = P[i]; 43 centerIndex = i; 44 } 45 } 46 47 return s.substring((centerIndex - 1 - maxLen)/2, maxLen); 48 }
什么是O(n)的时间复杂度,明明是for套了一个inner loop while啊,解释在这里:
In each step, there are two possibilities. If P[ i‘ ] ≤ R – i, we set P[ i ] to P[ i’ ] which takes exactly one step. Otherwise we attempt to change the palindrome’s center to i by expanding it starting at the right edge,
R. Extending R (the inner while loop) takes at most a total of N steps, and positioning and testing each centers take a total of N steps too. Therefore, this algorithm guarantees to finish in at most 2*N steps, giving a linear time solution.
说实话,我也没太看明白,还在理解中。不过原文作者说了,这个算法在面试中能想出来简直是不可能的,大家权当深入理解下manacher算法,有点印象,在给出一个O(n2) 之后,面试官follow-up提问的时候,可以讲讲这个思路。
LeetCode(5) : Longest Palindromic Substring
标签:
原文地址:http://www.cnblogs.com/lupx/p/leetcode-5.html