The standard equation of a plane is
A x + B y + C z + D = 0
where (A,B,C) is the unit normal. The value of D is determined by substituting in the known point (Px,Py,Pz) on the plane, namely
D = - (A Px + B Py + C Pz)
For a vertex (Qx,Qy,Qz) the expression
side(Q) = A Qx + B Qy + C Qz + D
can be used to determine which side of the plane the vertex lies on. If it is positive the point lies on the same side as the normal, if negative it lies on the other side, if zero it lies on the plane.
After determining if an edge intersects the cutting plane it is necessary to calculate the intersection point as that will become a vertex of the clipped facet. Let the edge be between two points P0 and P1, the equation of the points along the line segment
P = P0 + u(P1 - P0)
where u lies between 0 and 1. Substituting this into the expression for the plane
A (P0x + u (P1x - P0x)) + B (P0y + u (P1y - P0y)) + C (P0z + u (P1z - P0z)) + D = 0
Solving for u
u = - side(P0) / (side(P1) - side(P0))
Substituting this into the equation of the line gives the actual intersection point.
There are 8 different cases to consider, they are illustrated in the table below and appear in order in the source code. The top two cases are when all the points are on either side of the clipping plane. The three cases on the left are when there is only one vertex on the clipping side of the plane, the three cases on the right occur when there are two vertices on the clipping side of the plane. 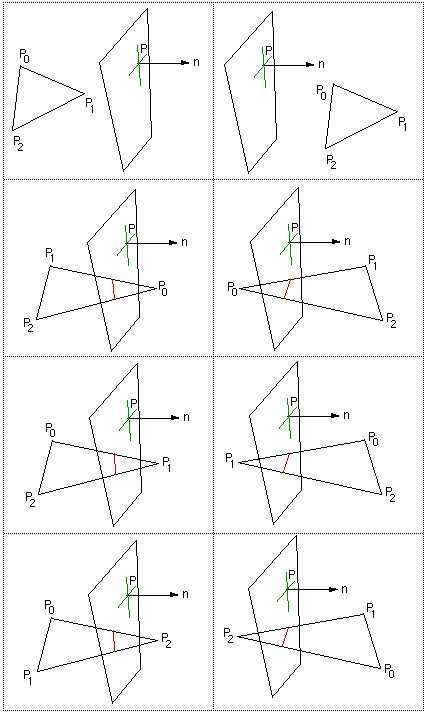
Note
When there is only one point on the clipping side the resulting facet has 4 vertices, if the underlying database only deals with 3 vertex facets then this can be bisected using a number of methods.
When the facets to be clipped have more than 3 vertices then they can be subdivided first and each segment clipped individually.
The algorithm as presented has no divide by zero problems
The source below does the clipping in place, the order in which the vertices are calculated is important for the 3 cases when there is one point on the clipping side of the plane.


提取三角网格轮廓线—基于法截线,布布扣,bubuko.com
原文地址:http://www.cnblogs.com/junzhang-uestc/p/3842882.html