标签：

这段时间阅读了英文版的NVidia官方的《The CG Tutorial》，通过它来学习基本的图形学知识和着色器编程。

在此做一个阅读记录。

动画 Animation

一、基于时间的运动 Movement in Time

实现动画渲染，需要应用程序对时间进行监测，并将它作为一个全局变量传递给着色器。

尽量在GPU上使用顶点着色器执行动画计算是一种高效的动画实现方式，它能够释放CPU，让CPU处理更多的复杂计算，比如碰撞检测，人工智能与游戏玩法。

二、一个做脉冲运动的对象 A Pulsating Object

1.　　简介

下面会展示一个如何让一个对象周期性膨胀变形的例子。这个例子的目标是将时间作为输入参数，然后根据时间修改对象几何体的顶点位置。更确切地说，你需要沿着表面法线移动表面顶点的位置。

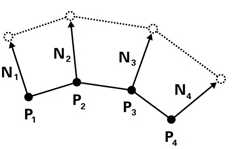
根据时间的变化，改变顶点位移Displacement的幅度，就可以创建一个膨胀或脉冲效果。

2.　　位移计算 Displacement Calculation

在上述动画实现的过程中，一个重要的过程是计算顶点在法线方向上的位移displacement。你可以为displacement选择一个你喜欢的函数，比如：

displacement = time

也许你不希望物体随时间无限变大，那么你可以选择使用一个周期函数来计算displacement，比如sin函数：

displacement = 0.5 * (sin(time) + 1)

• 在着色器中，sin/cos函数的效率等同于加减法。

此外，你还可以通过为displacement增加参数来控膨胀的幅度、频率，甚至改变膨胀效果：

displacement = scaleFactor * 0.5 * (sin(position.y * frequency * time) + 1)

• scaleFactor表示了膨胀的幅度
• frequency表示膨胀的频率
• position.y用于让不同的顶点具有不同的膨胀幅度，也可以替换成其他任意与顶点属性有关的函数
• 在这里，我们可以对scaleFactor * 0.5做预计算，并将它储存为一个全局变量，以降低顶点着色器的运算压力。

三、粒子系统 Particle Systems

1.　　简介

有时，不同于让顶点在网格中运动，我们希望把每一个顶点都作为一个独立的对象，或者称为一个粒子。而遵循某种规律运动的粒子的集合被称为粒子系统。粒子系统会随着时间发生变化。

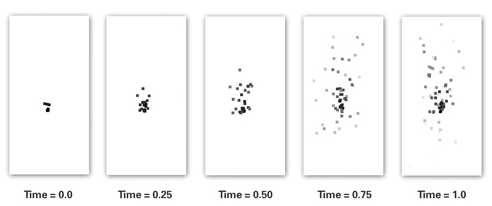
粒子的运动规律可以使用一个方程来描述，比如物理中的简单矢量运动学方程：

p_final = p_initial + v * t + 0.5 * a * t²

• p_final是粒子的最终位置
• p_initial­是粒子的初始位置
• v是粒子的初始速度
• a是粒子的加速度
• t是时间

2.　　计算粒子位置

在程序中，通过监测全局时间globaTime并将它作为统一参数传递给顶点着色器，当每个粒子被创建时，粒子创建的时间被作为一个变量tInitial传递给顶点着色器。为了知道粒子被激活的时间，你需要使用globaTime减去tInitial：

float t = globaTime - tInitial

再将t代入上一节中的公式：

float4 pFinal = pInitial + vInitial * t + 0.5f * acceleration * t * t

对象空间的位置还需要被转换到裁剪空间：

oPosition = mul(ModelViewProjectionMatrix, pFinal)

3.　　计算粒子尺寸 Computing the Particle Size

顶点着色器提供了一个名为PSIZE的输出语义Semantic用于表示顶点的尺寸，当你将一个点Point渲染到屏幕中时，具有该语义的输出参数将会决定该点在像素上的宽高。

4.　　美化粒子系统 Dressing Up Your Particle System

我们可以通过使用点精灵Point Sprites提升粒子的外观。使用点精灵时，硬件将会把每个点当作由四个顶点组成矩形来渲染，而不是一个单独的顶点。点精灵的每个顶点会被自动分配纹理坐标，它允许你通过纹理贴图改变粒子的外观。

点精灵能够在不绘制额外三角形的情况下创建复杂的几何效果。

四、关键帧插值 Key-Frame Interpolation

1.　　简介

关键帧这个术语来自卡通动画。画家在绘制动画时，会先勾勒出一个粗糙的帧序列动画，其中并没有包含每一帧的画面，而只有重要的，也就是“关键”的帧。随后，画家会补上缺失的帧。有了关键帧做参考，这些中间帧会更容易画。

计算机动画也使用了类似的技术，3D建模师会为动画角色的每个姿势制作一个关键帧。每个关键帧都需要使用相同个数的顶点，且每个顶点必须互相对应。也就是一个关键帧中的顶点必须能够对应到这个模型其他关键帧中相同的点。对于这种关键帧模型，游戏会取模型的两个关键帧，然后将其中每对对应的顶点混合。

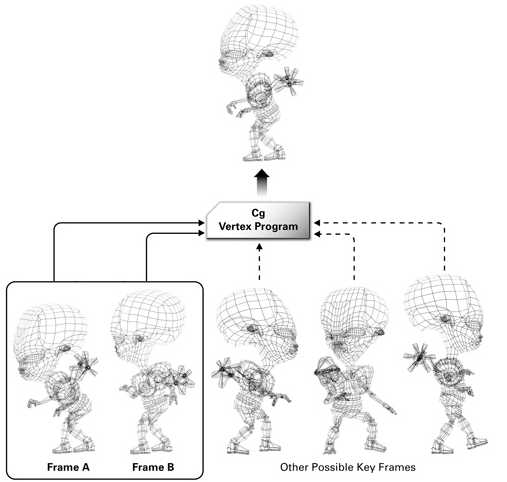
关键帧插值假定了顶点在每个关键帧中的个数和顺序都是相同的，这样一来就能够保证顶点着色器总能够正确地将顶点进行配对与混合。

2.　　插值方法 Interpolation Approaches

插值的方法有很多，常见的两种是线性插值和二次插值。

1)        线性插值 Linear Interpolation

通过线性插值，位置会以固定的速率转。线性插值公式为：

BlendedPosition = positionA * (1 - f) + position * f

2)        二次插值 Quadratic Interpolation

如果想让转换速率根据时间变化，可以采用二次插值，公式为：

IntermediatePosition = positionA * (1 – f * f) + position * f * f

3)        其他插值方法

除了上诉两种插值公式以外，你还可以使用阶梯函数、样条函数或者指数函数进行插值。

3.　　带有光照的关键帧插值 Key-Frame Interpolation with Lighting

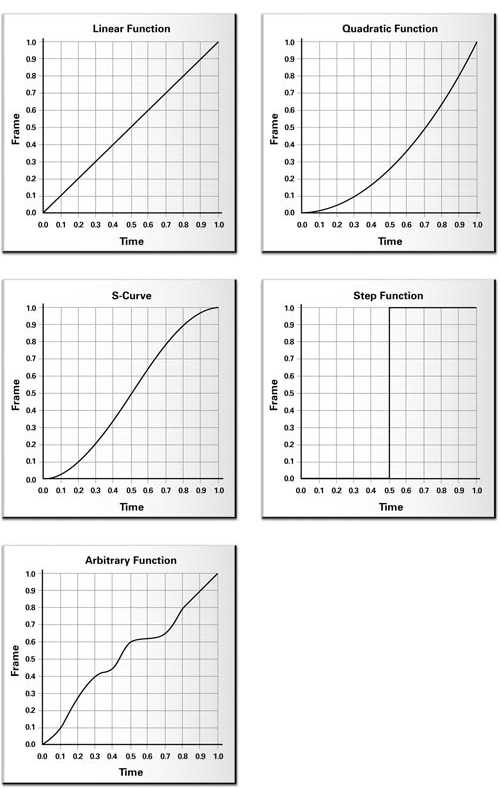
当你需要对关键帧模型进行照明时，关键帧插值就不仅涉及到位置的混合，还包括了顶点法线的混合。混合后的法线可能不再是单位向量，因此此时需要对它进行标准化。

五、顶点蒙皮 Vertex Skinning

1.　　简介

动画的另一种实现方式是顶点蒙皮，这项技术也被称为“矩阵调色混合“。

不同于关键帧动画，顶点蒙皮动画存储了模型的一个默认姿势和大量用于旋转与移动默认姿势的多边形网格子区域的矩阵，通常，这些矩阵变换被称为骨骼Bones。

每个默认姿势中多边形网格的顶点都被一个或多个这种矩阵所控制，每个矩阵都没指定了一个权重因子，用于指明当前矩阵对顶点的影响程度。假定每个顶点的所有控制矩阵的权重和为1。

当你需要渲染拥有顶点蒙皮的模型时，你需要使用每个顶点的骨骼集合中的所有矩阵对这个顶点执行变换，再将它们按照权重进行混合，得到的位置就是蒙皮顶点的位置。

当所有的矩阵都是单位矩阵时，模型展现的就是默认姿势——通常是站立面向前方，手脚分开向外伸展。

2.　　通过矩阵构建姿势 Constructing Poses from Matrices

通过控制矩阵，你能够创建出不一样的姿势。3D建模师需要将矩阵和对应的权重分配到模型的默认姿势上，而创建姿势的过程就变成了操作矩阵的过程，而不是控制每个独立的顶点。通过这种方式，改变模型的姿势与制作动画变得非常简单。

通常，影响一个顶点的矩阵不会超过4个。

对于角色模型来说，最重要的矩阵被用来代表人物身体中骨骼的移动和旋转，因此顶点蒙皮矩阵被称为骨骼。而顶点则代表了皮肤上的点。

3.　　光照 Lighting

同关键帧插值动画一样，在启用光照时，顶点蒙皮动画也需要对法向量进行变换。需要注意的是你需要对每个法向量只需要使用旋转缩放矩阵而不是原矩阵进行变换。同时，混合后也需要对法向量进行标准化。

4.　　在存储需求上对比关键帧动画 Storage Requirements Compared with Key Frames

关键帧动画中，每个姿势都需要不同的顶点位置与法向量集合，当角色动作很多时，采用这种方式存储动画是非常不明智的。

顶点蒙皮动画，只需要存储一个默认姿势的顶点位置与法向量集合以及每个姿势的矩阵。通常对一个模型来说，因为矩阵的个数远少于顶点个数，所以使用顶点蒙皮的方式存储动画需要的空间远远少于关键帧动画。

存储顶点蒙皮动画时，每个顶点还需要额外存储控制该顶点的矩阵索引，以及相应的权重因子。

顶点蒙皮非常适合用于存储和回放动作捕捉序列。我们可以将每一个动作捕捉的帧作为骨骼矩阵集合存储起来，并将它应用在拥有相同默认姿势的不同模型上。反向运动学求解器Inverse Kinematics Solver也可以通过生成骨骼矩阵来实现。反向运动学求解器的目的是找到一个能让一个姿势真实自然地过渡到另一个姿势的增量骨骼矩阵序列。

《The CG Tutorial》阅读笔记——动画 Animation

标签：

原文地址：http://www.cnblogs.com/dbylk/p/4793480.html