标签:
题意:在一面墙上贴海报,有先后顺序,问最后有多少张不同的海报(指的是没被覆盖或者只是部分覆盖的海报)
分析:这题数据范围很大,直接搞超时+超内存,需要离散化:离散化简单的来说就是只取我们需要的值来用,比如说区间[1000,2000],[1990,2012] 我们用不到[-∞,999][1001,1989][1991,1999][2001,2011][2013,+∞]这些值,所以我只需要1000,1990,2000,2012就够了,将其分别映射到0,1,2,3,在于复杂度就大大的降下来了所以离散化要保存所有需要用到的值,排序后,分别映射到1~n,这样复杂度就会小很多很多。而这题的难点在于每个数字其实表示的是一个单位长度(并非一个点),这样普通的离散化会造成许多错误(包括我以前的代码,poj这题数据奇弱)。给出下面两个简单的例子应该能体现普通离散化的缺陷:
例子一:1-10 1-4 5-10
例子二:1-10 1-4 6-10
普通离散化后都变成了[1,4][1,2][3,4]
配上图(例子一):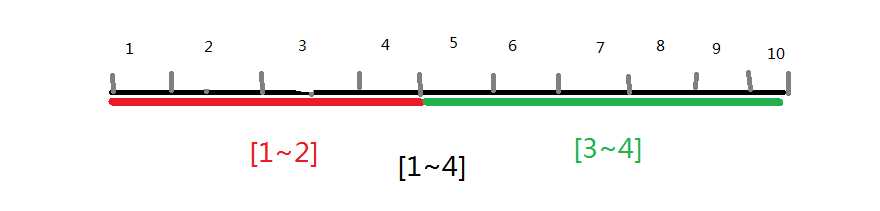
为了解决这种缺陷,我们可以在排序后的数组上加些处理,比如说[1,2,6,10]
如果相邻数字间距大于1的话,在其中加上任意一个数字,比如加成[1,2,3,6,7,10],然后再做线段树就好了。 --copy from Notonlysuccess
收获:离散化技巧
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
const int N = 1e4 + 10;
const int INF = 0x3f3f3f3f;
int ans;
struct ST {
int col[N<<4];
bool vis[N];
void init(void) {
memset (col, -1, sizeof (col));
memset (vis, false, sizeof (vis));
}
void push_down(int rt) {
if (col[rt] != -1) {
col[rt<<1] = col[rt<<1|1] = col[rt];
col[rt] = -1;
}
}
void updata(int ql, int qr, int c, int l, int r, int rt) {
if (ql <= l && r <= qr) {
col[rt] = c; return ;
}
push_down (rt);
int mid = (l + r) >> 1;
if (ql <= mid) updata (ql, qr, c, lson);
if (qr > mid) updata (ql, qr, c, rson);
}
void query(int l, int r, int rt) {
if (col[rt] != -1) {
if (!vis[col[rt]]) {
ans++; vis[col[rt]] = true;
}
return ;
}
if (l == r) return ;
int mid = (l + r) >> 1;
query (lson);
query (rson);
}
}st;
int L[N], R[N];
int X[N<<2];
int main() {
int T, n; scanf("%d",&T);
while (T --) {
scanf("%d",&n);
int tot = 0;
for (int i=0; i<n; ++i) {
scanf ("%d%d", &L[i], &R[i]);
X[tot++] = L[i];
X[tot++] = R[i];
}
sort (X, X+tot);
int k = 1;
for (int i=1; i<tot; ++i) {
if (X[i] != X[i-1]) X[k++] = X[i];
}
for (int i=k-1; i>=1; --i) {
if (X[i] != X[i-1] + 1) X[k++] = X[i-1] + 1;
}
sort(X, X+k);
st.init ();
for (int i=0; i<n; ++i) {
int ql = lower_bound (X, X+k, L[i]) - X;
int qr = lower_bound (X, X+k, R[i]) - X;
st.updata (ql, qr, i, 0, k, 1);
}
ans = 0;
st.query(0, k, 1);
printf("%d\n", ans);
}
return 0;
}
线段树+离散化 POJ 2528 Mayor's posters
标签:
原文地址:http://www.cnblogs.com/Running-Time/p/4797442.html