标签:
称号:
Maple trees |
| Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) |
| Total Submission(s): 177 Accepted Submission(s): 63 |
Problem Description There are a lot of trees in HDU. Kiki want to surround all the trees with the minimal required length of the rope . As follow, 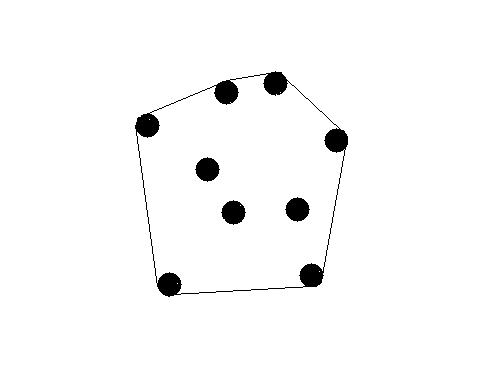 To make this problem more simple, consider all the trees are circles in a plate. The diameter of all the trees are the same (the diameter of a tree is 1 unit). Kiki can calculate the minimal length of the rope , because it‘s so easy for this smart girl. But we don‘t have a rope to surround the trees. Instead, we only have some circle rings of different radius. Now I want to know the minimal required radius of the circle ring. And I don‘t want to ask her this problem, because she is busy preparing for the examination. As a smart ACMer, can you help me ? 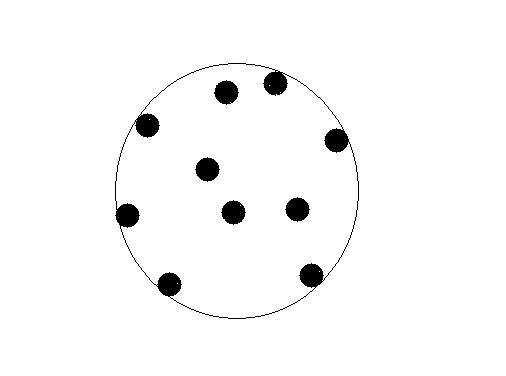 |
Input The input contains one or more data sets. At first line of each input data set is number of trees in this data set n (1 <= n <= 100), it is followed by n coordinates of the trees. Each coordinate is a pair of integers, and each integer is in [-1000, 1000], it means the position of a tree’s center. Each pair is separated by blank. Zero at line for number of trees terminates the input for your program. |
Output Minimal required radius of the circle ring I have to choose. The precision should be 10^-2. |
Sample Input 2 1 0 -1 0 0 |
Sample Output 1.50 |
Author zjt |
Recommend lcy |
题目分析:
求凸包的最小覆盖圆的半径。事实上就是在求完凸包以后再求一下最小覆盖圆即可了。
这道题须要用到下面的一些知识:
1、关于钝角三角形,假设c是斜边,那么必定有a^2 + b^2 < c^2的证明。
2、由三角形的三个顶点求一个三角形的面积。
已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。该三角形的面积为:
S = ( (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1) ) / 2 ;
△A1A2A3 边界构成逆时针回路时取+ , 顺时针时取 -。
另外在求解的过程中。不须要考虑点的输入顺序是顺时针还是逆时针,相除后就抵消了。
3、
凸包+最小圆覆盖
枚举随意3点找其最小覆盖圆
(当为钝角三角形时不是外接圆,而是以其最长边为直径的圆)。
当为外接圆时,半径公式为r=abc/4s;(推导为例如以下:
由正弦定理,a/sinA=b/sinB=c/sinC=2R,得sinA=a/(2R),
又三角形面积公式S=(bcsinA)/2,所以S=(abc)/(4R),故R=(abc)/(4S).这道题还须要注意的是:
1、在使用完graham求最小凸包以后。尽量让这个凸包闭合。即p[n] = p[0]。
代码例如以下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const double epsi = 1e-8;
const double pi = acos(-1.0);
const int maxn = 101;
struct PPoint{//结构体尽量不要定义成Point这样的,容易和C/C++本身中的变量同名
double x;
double y;
PPoint(double _x = 0,double _y = 0):x(_x),y(_y){
}
PPoint operator - (const PPoint& op2) const{
return PPoint(x - op2.x,y - op2.y);
}
double operator^(const PPoint &op2)const{
return x*op2.y - y*op2.x;
}
};
inline int sign(const double &x){
if(x > epsi){
return 1;
}
if(x < -epsi){
return -1;
}
return 0;
}
inline double sqr(const double &x){
return x*x;
}
inline double mul(const PPoint& p0,const PPoint& p1,const PPoint& p2){
return (p1 - p0)^(p2 - p0);
}
inline double dis2(const PPoint &p0,const PPoint &p1){
return sqr(p0.x - p1.x) + sqr(p0.y - p1.y);
}
inline double dis(const PPoint& p0,const PPoint& p1){
return sqrt(dis2(p0,p1));
}
int n;
PPoint p[maxn];
PPoint convex_hull_p0;
inline bool convex_hull_cmp(const PPoint& a,const PPoint& b){
return sign(mul(convex_hull_p0,a,b)>0)|| (sign(mul(convex_hull_p0,a,b)) == 0 && dis2(convex_hull_p0,a) < dis2(convex_hull_p0,b));
}
int convex_hull(PPoint* a,int n,PPoint* b){
int i;
for(i = 1 ; i < n ; ++i){
if(sign(a[i].x - a[0].x) < 0 || (sign(a[i].x - a[0].x) == 0 && sign(a[i].y - a[0].y) < 0)){
swap(a[i],a[0]);
}
}
convex_hull_p0 = a[0];//这两行代码不要顺序调换了..否则会WA
sort(a,a+n,convex_hull_cmp);
b[0] = a[0];
b[1] = a[1];
int newn = 2;
for(i = 2 ; i < n ; ++i){
while(newn > 1 && sign(mul(b[newn-1],b[newn-2],a[i])) >= 0){
newn--;
}
b[newn++] = a[i];
}
return newn;
}
/**
* 有一个三角形的三个点来计算这个三角形的面积
*/
double crossProd(PPoint A, PPoint B, PPoint C) {
return (B.x-A.x)*(C.y-A.y) - (B.y-A.y)*(C.x-A.x);
}
int main(){
while(scanf("%d",&n)!=EOF,n){
int i;
for(i = 0 ; i < n ; ++i){
scanf("%lf %lf",&p[i].x,&p[i].y);
}
/**
* 处理节点数仅仅有1、2的情况
*/
if(n == 1){
printf("0.50\n");
continue;
}
if(n == 2){
printf("%.2lf\n",dis(p[0],p[1])/2 + 0.5);
continue;
}
/**
* 当结点数>=3时,用graham算法来求最小凸包
*/
n = convex_hull(p,n,p);
p[n] = p[0];//记得要收尾相接,否则可能会出错
int j;
int k;
double maxr = -1;//用于求最小覆盖圆的半径
double r;
/**
* 枚举凸包中的随意三个点.
* 假设这三个点形成的外接圆的半径最大,
* 那么这个就是我们所要找的凸包的最小覆盖圆
*/
for(i = 0 ; i < n ; ++i){
for(j = i+1 ; j < n ; ++j){
for(k = j+1 ; k <= n ; ++k){//注意,这里的k是 <= n
double a = dis(p[i],p[j]);
double b = dis(p[i],p[k]);
double c = dis(p[j],p[k]);
//假设这三个点所形成的是钝角三角形
if(a*a+b*b < c*c || a*a+c*c < b*b || b*b+c*c < a*a){
r = max(max(a,b),c)/2;//那么这时候的半径等于最长边的一半
}else{//假设是直角三角形||锐角三角形
double s = fabs(crossProd(p[i],p[j],p[k]))/2;//由定理1求得面积
r = a*b*c/(4*s);//三角形的外接圆公式
}
if(maxr < r){//假设眼下存储的最大半径<当前外接圆的半径
maxr = r;//则更新眼下的最大半径
}
}
}
}
printf("%.2lf\n",maxr + 0.5);//输出凸包的最小覆盖圆的最大半径
}
return 0;
}
版权声明:本文博主原创文章,博客,未经同意不得转载。
(hdu step 7.1.5)Maple trees(凸包的最小半径寻找掩护轮)
标签:
原文地址:http://www.cnblogs.com/yxwkf/p/4798469.html