Redis研究-3.4 为何使用Redis跳跃表

标签：

好几天没把笔记整理上来了，一个是这几天在忙着一些投标以及项目论文的事情，哈哈，还有么 就是画图也是比较耗费我时间的，如果有好的画图建议或者工具，麻烦推荐一下，谢谢。废话不多说，直接进入今天的两个主题：二叉搜索树，平衡二叉树。

1.二叉搜索树（BST）

二叉搜索树的定义很简单：是二叉树，且满足两个条件：如果有左孩子，则左孩子的关键字一定不大于父节点的关键字，如果有右孩子，则右孩子的关键字不小于父节点的关键字。同时，左右子树都是二叉搜索树。

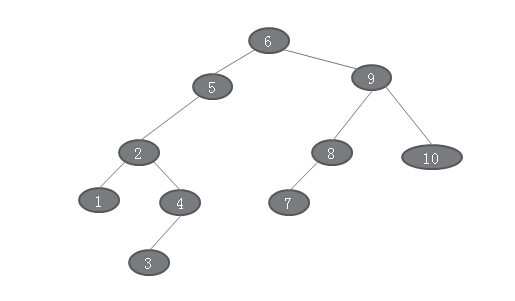
                                                    BST_1

中序遍历得到的结果是：1、2、3、4、5、6、7、8、9、10

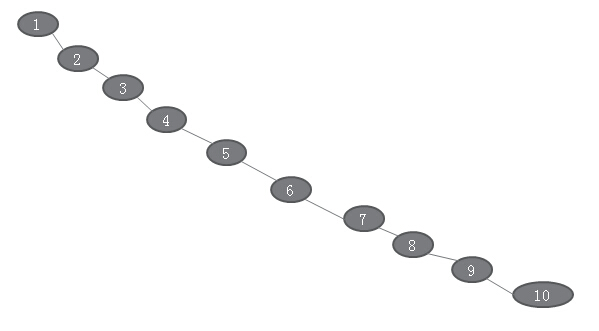
                                                   BST_2

中序遍历得到的结果是：1、2、3、4、5、6、7、8、9、10

现在有一个场景，加入我要在这颗树中查找一个关键字11，如果没有的话，则加入到这颗树中，查询步骤是：

1.针对BST_1,根节点是6，因为11大于6，则查找根节点的右孩子（因为二叉搜索树的右孩子的关键字不小于父节点）；

2.右孩子的值是9，小于11，继续查他的右孩子；

3.右孩子的值是10，小于11，继续查他的右孩子；

4.因为没有右孩子了，所以，需要将其添加为右孩子。

针对BST_2,我们只需要一直找右孩子就可以了。我们再看一个二叉搜索树：

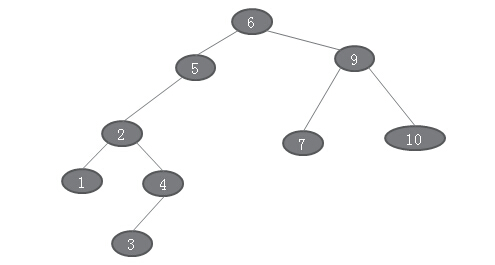
                                         BST3

中序遍历得到的结果是：1、2、3、4、5、6、7、9、10

现在我要查找一个节点，其中的关键字是8的一个节点，如果不在这颗树中，则把它加到树中作为一个节点：

1.根节点是6，小于8，找右孩子；

2.右孩子的值是9大于8，找他的左孩子；

3.左孩子的值7小于8，找他的右孩子；

4.因为没有右孩子了，所以，将其添加为7的右孩子。

从上面几个过程中我们发现一个规律：动态查找过程中，我们不需要重构这个结构，只是在叶子节点上进行操作，非常方便。

那如果要删除一个节点呢？

删除节点的时候，有几种情况需要考虑：

1.该节点是叶子节点，因此，不用重构；

2.该节点只有左子树或者右子树，则把左子树或者右子树的根，接到删除节点的父节点上就可以了；

3.如果该节点两者都有呢？

我们一个一个的来看：

1.该节点是叶子节点。

我们要删除BST3中的节点7，则先按照查询步骤找到这个节点，发现他没有左子树，也没有右子树，则直接删除，并把该节点的父节点的左孩子或者右孩子（取决于该节点是左孩子还是右孩子）清空即可。

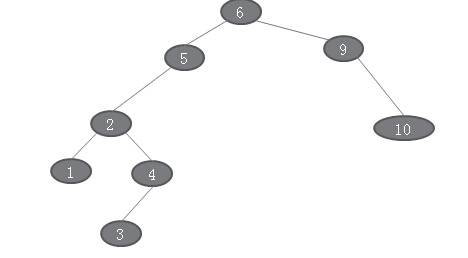
2.该节点只有左子树。

我们要删除BST3中的节点4，则先按照查询步骤找到这个节点，发现他只有左子树，因此，只要删除该节点，并把该节点的左孩子放在改节点的位置即可。

3.该节点只有右子树：

我们要删除BST2中的节点5，则先按照查询步骤找到这个节点，发现他只有由子树，因此，只要删除该节点，并把该节点的右孩子放在该节点的位置即可。

4.该节点有左子树，也有右子树。

我们现在要删除BST1中的根节点，则中序遍历这个节点的左子树，得到的此节点前的那个节点，就是要删除节点的前驱。

比如上述根节点的左子树的中序遍历是：1、2、3、5，则，我是要删除节点6的前驱，将该前驱替代要删除的节点的位置，并设置左指向和右指向即可。

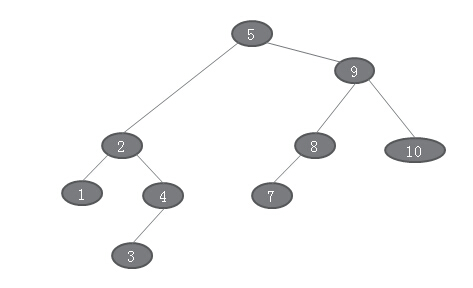
，我们现在再来看一BST。

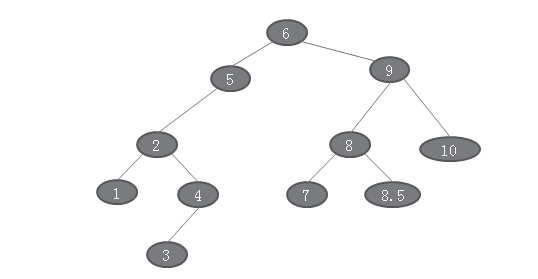
现在我要删除节点9，按照上面的步骤，9有左右孩子，因此，先做9的左子树的中序遍历，找到9的前驱是8.5,然后来替换。最终得到结果是：

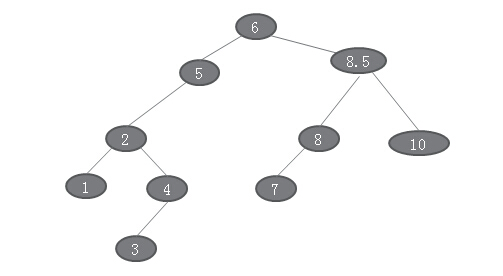
，说了那么多，还是上上代码吧，这次用java代码：

package com.tang.bst;

import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;

public class BST<Key extends Comparable<Key>> {
	BSTNode<Key> root;

	public BST() {
	}

	/**
	 * 插入一个节点
	 * 
	 * @param data
	 *            节点的数据
	 * @return
	 */
	public boolean insert(Key data) {
		if (null == data)
			return false;
		if (null == this.root) {
			this.root = new BSTNode<Key>(data);
			this.root.parent = null;
			this.root.leftChild = null;
			this.root.rightChild = null;
			return true;
		} else {
			return insertBST(this.root, data);
		}

	}

	private boolean insertBST(BSTNode<Key> node, Key data) {
		// 左分支，右分支的判断
		int lOrR = node.data.compareTo(data);
		if (lOrR == 0) {
			return false;
		} else if (lOrR < 0) {
			// 右子树
			if (null == node.rightChild) {
				BSTNode<Key> rChild = new BSTNode<Key>(data);
				rChild.parent = node;
				node.rightChild = rChild;
				return true;
			} else {
				return insertBST(node.rightChild, data);
			}
		} else {
			// 左子树
			if (null == node.leftChild) {
				BSTNode<Key> lChild = new BSTNode<Key>(data);
				lChild.parent = node;
				node.leftChild = lChild;
				return true;
			} else {
				return insertBST(node.leftChild, data);
			}
		}
	}

	/**
	 * 在这棵树中，指定一个节点，然后开始非递归方式中序遍历以这个节点为根节点的二叉树
	 * 
	 * @param node
	 *            指定为根节点的节点
	 * @return
	 */
	public List<BSTNode<Key>> noRecurseInOrderTraverse(Key data) {
		if (null == this.root)
			return null;
		BSTNode<Key> beginRoot = null;
		if (null == data) {
			beginRoot = this.root;// 如果没有指定节点为根节点，那么就从这棵树的根节点开始
		} else {
			BSTNode<Key> sNode = searchBST(this.root, data);
			beginRoot = sNode;
		}
		List<BSTNode<Key>> stack = new ArrayList<BSTNode<Key>>();
		List<BSTNode<Key>> retStack = new ArrayList<BSTNode<Key>>();
		if (null != beginRoot) {
			stack.add(beginRoot);
		}

		while (!stack.isEmpty()) {
			while (beginRoot != null && null != beginRoot.leftChild) {
				beginRoot = beginRoot.leftChild;
				stack.add(beginRoot);
			}
			if (!stack.isEmpty()) {
				BSTNode<Key> tmpNode = stack.get(stack.size() - 1);
				stack.remove(stack.size() - 1);
				retStack.add(tmpNode);
				if (tmpNode != null && null != tmpNode.rightChild) {
					beginRoot = tmpNode.rightChild;
					stack.add(beginRoot);
				}
			}
		}
		return retStack;
	}

	/**
	 * 查找指定的节点，如果没有，则将他加入到这颗树上
	 * 
	 * @param data
	 * @return 0:表示在原树上就有,1:表示添加进去的新节点,-1:表示查询中出错
	 */
	public boolean search(Key data) {
		if (null == data) {
			return false;
		}
		if (null == this.root) {
			return false;
		}
		return searchBST(this.root, data) == null ? false : true;
	}

	private BSTNode<Key> searchBST(BSTNode<Key> searhNode, Key data) {
		if (null == data) {
			return null;
		}
		if (null == searhNode) {
			return null;
		}
		int lOrR = searhNode.data.compareTo(data);
		if (lOrR > 0) {
			// 要往左子树去找
			return searchBST(searhNode.leftChild, data);
		} else if (lOrR == 0) {
			// 已经找到了，直接返回去
			return searhNode;
		} else {
			// 要往右子树去找
			return searchBST(searhNode.rightChild, data);
		}

	}

	/**
	 * 查找指定的节点，如果没有的话，插入节点
	 * 
	 * @param data
	 * @return
	 */
	public boolean searchOrInsert(Key data) {
		return search(data) == false ? insert(data) : true;
	}

	/**
	 * 删除指定的节点
	 * 
	 * @param data
	 * @return
	 */
	public boolean delete(Key data) {
		if (null == this.root || null == data) {
			return false;
		}
		BSTNode<Key> node = searchBST(this.root, data);
		if (null == node) {
			return false;
		}
		BSTNode<Key> parent = node.parent;
		BSTNode<Key> leftChild = node.leftChild;
		if (null == node.rightChild) {
			// 因为没有右孩子，因此，只要重新接上她的左孩子就可以了
			if (null == parent) {
				// 说明他是根节点
				if (null != leftChild) {
					node.leftChild.parent = null;
				} else {
					this.root = null;
				}
			} else {
				node.parent.leftChild = leftChild;
			}
		} else if (null == node.leftChild) {
			// 因为没有左孩子，只要重新接上她的右孩子就可以了
			if (parent == null) {
				// 说明他就是根节点
				if (null != node.rightChild) {
					node.rightChild.parent = null;
				} else {
					this.root = null;
				}
			} else {
				node.parent.rightChild = node.rightChild;
			}
		} else {
			// 既有左子树，又有右子树
			// 中序遍历此节点的左子树，找到此节点的前驱
			// 此前驱的特点是，要么是叶子节点，要么是只有左节点
			System.out.println(node.rightChild==null);
			List<BSTNode<Key>> stack=noRecurseInOrderTraverse(node.leftChild.data);
			BSTNode<Key> preNode=stack.get(stack.size()-1);
			BSTNode<Key> rightNode=node.rightChild;
			node.data=preNode.data;
			if(preNode.leftChild!=null){
				node.leftChild=preNode.leftChild;
			}
			if(preNode.parent!=null){
				if(preNode.parent.leftChild.data.compareTo(preNode.data)==0){
					preNode.parent.leftChild=null;
				}else{
					preNode.parent.rightChild=null;//这里有问题
				}
			}
			node.rightChild=rightNode;
			System.out.println(node.rightChild==null);
		}

		return true;
	}

	public static void main(String[] args) {
		BST<Integer> bst = new BST<Integer>();
		bst.insert(new Integer(6));
		bst.insert(new Integer(5));
		bst.insert(new Integer(9));
		bst.insert(new Integer(2));
		bst.insert(new Integer(8));
		bst.insert(new Integer(10));
		bst.insert(new Integer(1));
		bst.insert(new Integer(4));
		bst.insert(new Integer(3));
		List<BSTNode<Integer>> stack = bst.noRecurseInOrderTraverse(null);
		for (Iterator<BSTNode<Integer>> iterator = stack.iterator(); iterator
				.hasNext();) {
			BSTNode<Integer> bstNode = (BSTNode<Integer>) iterator.next();
			System.out.print(bstNode.data + "---");
		}

		bst.delete(new Integer(5));

		System.out.println("删除之后");
		stack = bst.noRecurseInOrderTraverse(null);
		for (Iterator<BSTNode<Integer>> iterator = stack.iterator(); iterator
				.hasNext();) {
			BSTNode<Integer> bstNode = (BSTNode<Integer>) iterator.next();
			System.out.print(bstNode.data + "---");
		}
	}

}

通过上面的学习，我们可以看到，二叉搜索树受输入顺序影响很大，有可能就是形成了一个线性表，效率非常低。咋整呢？收看下一节，欢迎加qq:359311095讨论

Redis研究-3.4 为何使用Redis跳跃表

标签：

原文地址：http://my.oschina.net/u/197860/blog/504686