标签:
程序中的所有数在计算机内存中都是以二进制的形式
储存的。位运算说穿了,就是直接对整数在内存中的二进制位进行操作。比如,and运算本来是一个逻辑
运算符,但整数与整数之间也可以进行and运算。举个例子,6的二进制是110,11的二进制是1011,那么6 and 11的结果就是2,它是二进制对应位进行逻辑运算的结果(0表示False,1表示True,空位都当0处理)。
110
AND 1011
---------------
0010 --> 2
有人会说,计算6 and 11没有什么实际意义啊。这一系列的文章就将告诉你,位运算到底可以干什么,有些什么经典应用,以及如何用位运算优化你的程序。
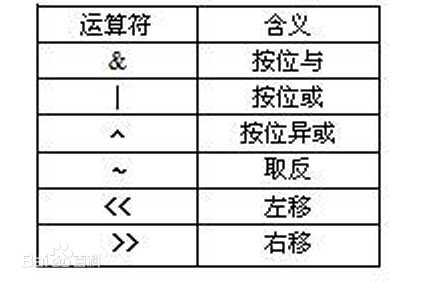
下面的a和b都是整数类型,则:
| 含义 | Pascal语言 | C语言 | Java |
|---|
| 按位与 |
a and b |
a & b |
a & b |
|---|
| 按位或 |
a or b |
a | b |
a | b |
|---|
| 按位异或 |
a xor b |
a ^ b |
a ^ b |
|---|
| 按位取反 |
not a |
~a |
~a |
|---|
| 左移 |
a shl b |
a << b |
a << b |
|---|
| 带符号右移 |
a shr b |
a >> b |
a >> b |
|---|
| 无符号右移 |
|
|
a>>> b |
|---|
注意C中的逻辑运算和位
运算符号是不同的。520|1314==3882,但520||1314=1,因为逻辑运算时520和1314都相当于True。同样的,!a和~a也是有区别的。
有时我们的程序需要一个规模不大的Hash表来记录状态。比如,做数独时我们需要27个Hash表来统计每一行、每一列和每一个小九宫
格里已经有哪些数了。此时,我们可以用27个小于2^9的整数进行记录。例如,一个只填了2和5的小九宫格就用数字18表示(二进制为000010010),而某一行的状态为511则表示这一行已经填满。需要改变状态时我们不需要把这个数转成二进制修改后再转回去,而是直接进行
位操作。在搜索时,把状态表示成整数可以更好地进行判重等操作。这道题是在搜索中使用位运算加速的经典例子。以后我们会看到更多的例子。
下面列举了一些常见的二进制位的变换操作。
功能 | 示例 | 位运算
----------------------+---------------------------+--------------------
去掉最后一位 | (101101->10110) | x shr 1
在最后加一个0 | (101101->1011010) | x shl 1
在最后加一个1 | (101101->1011011) | x shl 1+1
把最后一位变成1 | (101100->101101) | x or 1
把最后一位变成0 | (101101->101100) | x or 1-1
最后一位取反 | (101101->101100) | x xor 1
把右数第k位变成1 | (101001->101101,k=3) | x or (1 shl (k-1))
把右数第k位变成0 | (101101->101001,k=3) | x and not (1 shl (k-1))
右数第k位取反 | (101001->101101,k=3) | x xor (1 shl (k-1))
取末三位 | (1101101->101) | x and 7
取末k位 | (1101101->1101,k=5) | x and(1 shl k-1)
取右数第k位 | (1101101->1,k=4) | x shr (k-1) and 1
把末k位变成1 | (101001->101111,k=4) | x or (1 shl k-1)
末k位取反 | (101001->100110,k=4) | x xor (1 shl k-1)
把右边连续的1变成0 | (100101111->100100000) | x and (x+1)
把右起第一个0变成1 | (100101111->100111111) | x or (x+1)
把右边连续的0变成1 | (11011000->11011111) | x or (x-1)
取右边连续的1 | (100101111->1111) | (x xor (x+1)) shr 1
去掉右起第一个1的左边 | (100101000->1000) | x and (x xor (x-1))(或 x and (-x))
Pascal和C中的16进制表示
Pascal中需要在16进制数前加$符号表示,C中需要在前面加0x来表示。这个以后我们会经常用到。
http://baike.baidu.com/link?url=CbtldLO3RjKXWiDBruOltlTj4_UI3bRfDxt0jKs4dkHLiQ4hA6bDZfqFqv4zsGAXf2H0gGNhs6yNOjQv4HIiPa#4
位运算
标签:
原文地址:http://www.cnblogs.com/softidea/p/4799851.html
