标签:
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 722 Accepted Submission(s): 361
题目大意:让你求LCM(C(n,0),C(n,1),C(n,2)...C(n,n-1),C(n,n)),最后结果取模。
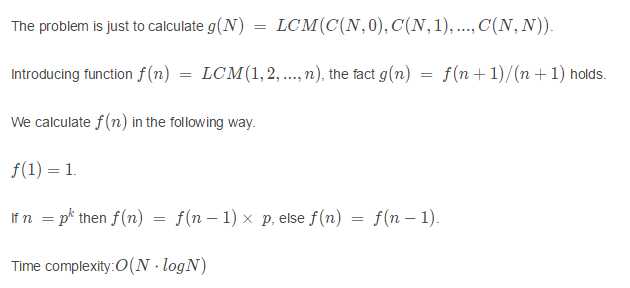
解题思路:其实只要有公式了,问题就很好解决了。f(n)是求1 - n的最小公倍数。这个是可以借鉴得。如果n是一个素数p的k次方,那么就乘以素数p。主要需要求逆元,和快速判断x是否为素数p的k次方。
#include<bits/stdc++.h>
using namespace std;
typedef long long INT;
const int maxn=1e6+20;
const INT MOD=1e9+7;
INT f[maxn],g[maxn],inv[maxn];
int p[maxn];
void init(){
for(int i=1;i<maxn;i++){
p[i]=i;
}
for(int i=2;i<maxn;i++){
if(p[i]==i){
for(int j=i+i;j<maxn;j+=i){
p[j]=i;
}
}
}
}
bool check(int x){
int d=p[x];
if(x>1){
while(x%d==0){
x/=d;
}
return x==1;
}
return false;
}
void get_f(){
f[1]=1;
for(int i=2;i<maxn;i++){
if(check(i)){
f[i]=f[i-1]*p[i]%MOD;
}else{
f[i]=f[i-1];
}
}
}
INT Powmod(INT a,INT n){
a%=MOD;
INT ret=1;
while(n){
if(n&1)
ret= ret * a % MOD;
n>>=1;
a = (a*a)%MOD;
}
return ret;
}
INT get_inv(int n){
return Powmod((INT)n,MOD-2);
}
INT get_g(int n){
return f[n+1]*get_inv(n+1)%MOD;
}
int main(){
int t,n;
init();
get_f();
scanf("%d",&t);
while(t--){
scanf("%d",&n);
INT ans=get_g(n);
printf("%lld\n",ans);
}
return 0;
}
HDU 5407——CRB and Candies——————【逆元+是素数次方的数+公式】
标签:
原文地址:http://www.cnblogs.com/chengsheng/p/4803332.html