标签:
只是简单的整形数据的四则运算,小伙伴们可以扩展到更多的运算,也不仅仅是整形数据O(∩_∩)O~,我经常把抽象数据类型的全部操作都包括进来,显得程序比较冗余,小伙伴们可以将不需要的操作去掉!而且要实现程序能够运行出来,要注意把需要的头文件包含进来
头文件:
#define STACK_INIT_SIZE 100 #define STACKINCREMENT 10 #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define MYOVERFLOW -2 typedef int Status; typedef char SElemtype;//用指定标识符Elemtype代表int类型,顾名思义表示元素类型为int型 typedef struct{ SElemtype *base;//在栈构造之前和销毁之后,base的值为NULL SElemtype *top;//栈顶!d=====( ̄▽ ̄*)b指针 int stacksize;//当前已分配的空间储存,以元素为单位 }SqStack; typedef int SElemtype1;//用指定标识符Elemtype代表int类型,顾名思义表示元素类型为int型 typedef struct{ SElemtype1 *base;//在栈构造之前和销毁之后,base的值为NULL SElemtype1 *top;//栈顶!d=====( ̄▽ ̄*)b指针 int stacksize;//当前已分配的空间储存,以元素为单位 }SqStack1; Status InitStack(SqStack1 &S);//构造一个空栈S Status GetTop(SqStack1 S, SElemtype1 &e);//若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR Status Push(SqStack1 &S, SElemtype1 e);//插入元素e为新的栈顶元素 Status Pop(SqStack1 &S, SElemtype1 &e);//若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR //-------上述操作属于函数的重载-------- //-------基本操作的函数原型说明-------- Status visit(SqStack S);//对栈进行遍历 void Create_Stack(SqStack &S);//创建一个栈 Status InitStack(SqStack &S);//构造一个空栈S Status DestroyStack(SqStack &S);//销毁栈S,S不再存在 Status ClearStack(SqStack &S);//把S置为空栈 Status StackEmpty(SqStack S);//若栈S为空栈,则返回TRUE,否则返回FALSE int StackLength(SqStack S);//返回S的元素个数,即栈的长度 Status GetTop(SqStack S, SElemtype &e); //若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR Status Push(SqStack &S, SElemtype e); //插入元素e为新的栈顶元素 Status Pop(SqStack &S, SElemtype &e); //若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR Status StackTraverse(SqStack S, Status(*visit)(SqStack S)); //从栈底到栈顶依次对栈中每个元素调用函数visit()一旦visit()失败,则操作失败 int EvaluateExpression(); //算术表达式求值的算符优先算法。设OPTR和OPND分别为运算符栈和运算数栈, //OP为运算符集合。
上述操作的实现:
#include "stdafx.h" Status InitStack(SqStack &S)//构造一个空栈S { S.base = (SElemtype *)malloc(STACK_INIT_SIZE*sizeof(SElemtype)); if (!S.base)exit(MYOVERFLOW); S.top = S.base; S.stacksize = STACK_INIT_SIZE; return OK; } Status DestroyStack(SqStack &S)//销毁栈S,S不再存在 { for (; S.top != S.base;){ SElemtype *temp = S.top; S.top--; delete temp; } delete S.base; S.stacksize = 0; return OK; } Status ClearStack(SqStack &S)//把S置为空栈 { S.top = S.base; return OK; } Status StackEmpty(SqStack S)//若栈S为空栈,则返回TRUE,否则返回FALSE { if (S.top == S.base)return TRUE; else return FALSE; } int StackLength(SqStack S)//返回S的元素个数,即栈的长度 { int length = 0; for (; S.top != S.base; S.top--)length++; return length; } Status GetTop(SqStack S, SElemtype &e) //若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR { if (S.top != S.base){ e = *(S.top - 1); return OK; } else return ERROR; } Status Push(SqStack &S, SElemtype e) //插入元素e为新的栈顶元素 { if (S.top - S.base >= S.stacksize){ S.base = (SElemtype *)realloc(S.base, (S.stacksize + STACKINCREMENT)*sizeof(SElemtype)); if (!S.base)exit(MYOVERFLOW); S.top = S.base + S.stacksize; S.stacksize += STACKINCREMENT; } *(S.top++) = e; return OK; } Status Pop(SqStack &S, SElemtype &e) //若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR { if (S.top != S.base){ e = *(--S.top); return OK; } else return ERROR; } Status visit(SqStack S)//对栈进行遍历1 { if (S.base){ cout << "the data of the Stack is:"; for (; S.top != S.base;) cout << *(--S.top) << " "; return OK; } else return ERROR; } Status StackTraverse(SqStack S, Status(*visit)(SqStack)) //从栈底到栈顶依次对栈中每个元素调用函数visit()一旦visit()失败,则操作失败 { if (visit(S))return OK; return ERROR; } void Create_Stack(SqStack &S)//创建一个栈 { InitStack(S); cout << "please input the length of the Stack:"; int len; cin >> len; cout << "please input the data of the Stack:"; for (int i = 1; i <= len; i++){ SElemtype temp; cin >> temp; Push(S, temp); } } //------------接下来的几个函数都是函数的重载--------------- //------------也可以用函数的模板,因为他们之--------------- //----------间仅有数据类型不同,实现过程完全相同----------- Status InitStack(SqStack1 &S)//构造一个空栈S { S.base = (SElemtype1 *)malloc(STACK_INIT_SIZE*sizeof(SElemtype1)); if (!S.base)exit(MYOVERFLOW); S.top = S.base; S.stacksize = STACK_INIT_SIZE; return OK; } Status GetTop(SqStack1 S, SElemtype1 &e)//若栈不空,则用e返回S的栈顶元素,并返回OK;否则返回ERROR { if (S.top != S.base){ e = *(S.top - 1); return OK; } else return ERROR; } Status Push(SqStack1 &S, SElemtype1 e)//插入元素e为新的栈顶元素 { if (S.top - S.base >= S.stacksize){ S.base = (SElemtype1 *)realloc(S.base, (S.stacksize + STACKINCREMENT)*sizeof(SElemtype1)); if (!S.base)exit(MYOVERFLOW); S.top = S.base + S.stacksize; S.stacksize += STACKINCREMENT; } *(S.top++) = e; return OK; } Status Pop(SqStack1 &S, SElemtype1 &e)//若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR { if (S.top != S.base){ e = *(--S.top); return OK; } else return ERROR; } Status In(char c, char *OP){//如果字符在数组中返回TRUE,否则返回FALSE for (int i = 0; i<=6;i++) if (c == OP[i])return TRUE; return FALSE; } char Precede(char ch, char c)//比较两个字符的优先级 { int i=0, j=0; char mychar[][7] = { //定义一个二维字符数组 { ‘>‘, ‘>‘, ‘<‘, ‘<‘, ‘<‘, ‘>‘, ‘>‘ }, { ‘>‘, ‘>‘, ‘<‘, ‘<‘, ‘<‘, ‘>‘, ‘>‘ }, { ‘>‘, ‘>‘, ‘>‘, ‘>‘, ‘<‘, ‘>‘, ‘>‘ }, { ‘>‘, ‘>‘, ‘>‘, ‘>‘, ‘<‘, ‘>‘, ‘>‘ }, { ‘<‘, ‘<‘, ‘<‘, ‘<‘, ‘<‘, ‘=‘, ‘ ‘ }, { ‘>‘, ‘>‘, ‘>‘, ‘>‘, ‘ ‘, ‘>‘, ‘>‘ }, { ‘<‘, ‘<‘, ‘<‘, ‘<‘, ‘<‘, ‘ ‘, ‘=‘ } }; char OP[] = { ‘+‘, ‘-‘, ‘*‘, ‘/‘, ‘(‘, ‘)‘, ‘#‘ }; for (; i <= 6;i++) if (ch == OP[i])break; for (; j <= 6;j++) if (c == OP[j])break;//得到两字符在数组中的位置 return mychar[i][j];//返回比较结果 } int Operate(int a, char theta, int b){ char OP[] = { ‘+‘, ‘-‘, ‘*‘, ‘/‘ };//比较是哪一个操作符 int i = 0; for (; i <= 3;i++) if (theta == OP[i])break; switch (i) { case 0://操作符的位置为0则为+,下面类似 return a + b; case 1: return a - b; case 2: return a*b; default: return a / b; } } int EvaluateExpression() //算术表达式求值的算符优先算法。设OPTR和OPND分别为运算符栈和运算数栈, //OP为运算符集合。 { cout << "please input the arithmetic and the end of it should be ‘#‘:" << endl; SqStack OPTR;//运算符栈 SqStack1 OPND;//运算数栈 InitStack(OPTR); Push(OPTR, ‘#‘);//这里用到了函数的重载,虽然都是对栈的操作,但操作数类型不同, InitStack(OPND); //运算符的数据元素为char,操作数的数据元素为int char c = getchar();char ch = ‘ ‘; char OP[] = { ‘+‘, ‘-‘, ‘*‘, ‘/‘, ‘(‘, ‘)‘, ‘#‘ }; int temp = 0; bool tag = FALSE; do{ if (!In(c, OP)){ temp = temp * 10 + c - 48; tag = TRUE;c = getchar(); }//如果对运算数的值进行了计算,则将tag设为TRUE else{ //说明如果后一个是运算符的话,可以将运算数压入栈 if (tag) { Push(OPND, temp); temp = 0; tag = FALSE; } GetTop(OPTR, ch); switch (Precede(ch, c)){ case ‘<‘: Push(OPTR, c); c = getchar();//前个运算符小于后果运算符,则入栈 break; case‘=‘: char x; Pop(OPTR, x); c = getchar();//两个运算符优先级相同,则出栈 break; case‘>‘: //前面一个运算符优先级高,则可进行计算 char theta; Pop(OPTR, theta); int a, b; Pop(OPND, a); Pop(OPND, b); Push(OPND, Operate(b, theta, a)); break; } } } while (c != ‘#‘); if (tag)Push(OPND, temp);//当遇到#时,还存在一次操作没有进行,将该操作进行完全 char theta; Pop(OPTR, theta); int a, b; Pop(OPND, a); Pop(OPND, b); Push(OPND, Operate(b, theta, a)); int result; GetTop(OPND, result); cout << "the result of the arithmetic is:" << result << endl; return result; }
主函数仅仅调用EvaluateExpression()函数,注意包含需要的头文件!
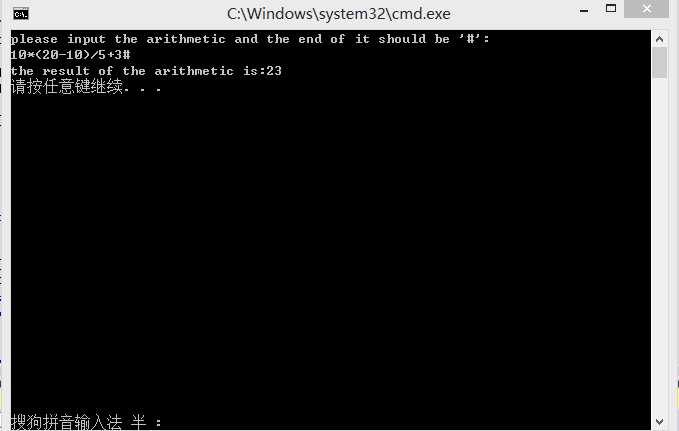
下面是运算结果:
标签:
原文地址:http://www.cnblogs.com/csudanli/p/4811708.html