Lucas定理 以及 C

标签：

最近碰到一题，问你求mod (p₁*p₂*p₃*……*p_l) ,其中n和m数据范围是1~1e18 , l ≤10 , p_i ≤ 1e5为不同的质数，并保证M=p₁*p₂*p₃*……*p_l ≤ 1e18 。

要解决这个问题首先需要Lucas定理 或者 C！解法。

Lucas定理：

我们令n=sp+q , m=tp+r . q ， r ≤ p

那么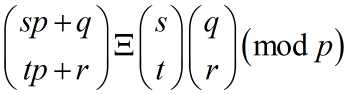，然后你只要继续对调用Lucas定理即可。

代码可以递归的去完成这个过程，其中递归终点为t = 0 ；

伪代码,时间O（log_p(n)*p)：

int Lucas (ll n , ll m , int p) {
        return m == 0 ? 1 : 1ll*comb (n%p , m%p , p) * Lucas (n/p , m/p , p) %  p ; 
}
//comb()函数中，因为q ， r ≤ p , 所以这部分暴力完成即可。

 Lucas定理证明：

证明资料：http://www.cut-the-knot.org/arithmetic/algebra/LucasTheorem.shtml

首先你需要这个算式: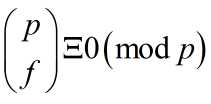，然后

(1 + x) ⁿ Ξ (1 + x) ^sp+q  Ξ ( (1 + x)^p)^s • (1 + x) ^q Ξ (1 + x^p) ^s • (1 + x) ^q   (mod p) ;

.

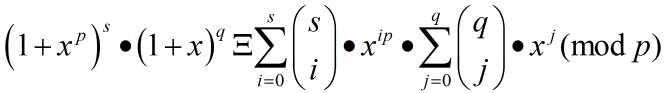所以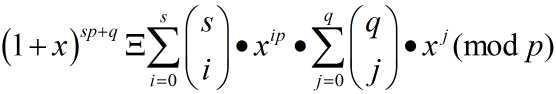，通过左右系数比较，你就会发现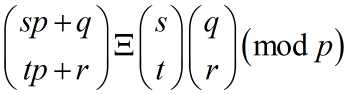，及i=t , j=r的时候。

Lucas定理 以及 C

标签：

原文地址：http://www.cnblogs.com/get-an-AC-everyday/p/4813692.html