标签:
题目:给定N个整数的序列{A1,A2,...,AN},求函数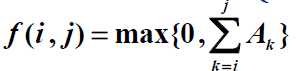
分析:A1,A2,...,AN是可正可负的整数序列,本题欲求从i到j的子序列和的最大值,不必求出是哪个序列。最容易想到的办法是暴力求解法,即求出所有子序列的和,找出它们的最大值,时间复杂度T(N)=O(N2);其次我们可以采取分而治之的方法把欲求解的问题递归分解为若干子问题,时间复杂度T(N)=O(NlogN);
算法一(暴力求解法):
int MaxSubseqsum1 (int A[],int N) { int ThisSum,MaxSum=0; int i,j; for(i=0;i<N;i++) //i是子列左端位置 { ThisSum=0; /* ThisSum是从A[i]到A[j]的子列和 */ for(j=i;j<N;j++)//j是子列右端位置 { ThisSum +=A[j]; if(ThisSum>MaxSum) MaxSum=ThisSum; } } return MaxSum; }
显然这种算法的时间复杂度为O(N2)
算法二(分治法):如果要是求出序列的位置的话,这将是最好的算法了(我们后面还会有个O(N)的算法,但是它不能求出最大子序列的位置)
最大子序列可能在三个地方出现,序列的左半部、右半部或者跨越序列中部而占据左右两部分。前两种情况递归求解,第三种情况的最大和可以通过求出左半部分最大和(包含左半部分最后一个元素)以及右半部分最大和(包含右半部分的第一个元素)相加而得到。
int MaxSubseqsum2(int A[],int N) { return maxSumRec(A, 0, N-1); } //递归法,复杂度是O(nlogn) int maxSumRec(int A[], int left, int right) { if (left == right) { if (A[left] > 0) return A[left]; else return 0; } int center = (left + right) / 2; int maxLeftSum = maxSumRec(A, left, center); //递归求解左半部分 int maxRightSum = maxSumRec(A, center+1, right); //递归求解右半部分 //求出左半部分包含最后一个元素的最大子序列和 int maxLeftBorderSum = 0, leftBorderSum = 0; for(int i = center; i >= left; i--) { leftBorderSum += A[i]; if (leftBorderSum > maxLeftBorderSum) maxLeftBorderSum = leftBorderSum; } //求出右半部分包含第一个元素的最大子序列和 int maxRightBorderSum = 0, rightBorderSum = 0; for(int j = center+1; j <= right; j++) { rightBorderSum += A[j]; if (rightBorderSum > maxRightBorderSum) maxRightBorderSum = rightBorderSum; } return max3(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum); } //求出三者中的最大值 int max3(int a, int b, int c) { int max=a; if (max<b) max=b; if (max<c) max=c; return max; }
分治法的原理图如下:
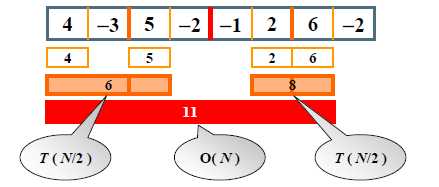
推算算法的时间复杂度,求解整个整数序列可分写为求解左半部分、右半部分以及跨越序列中部的子序列:T(N)=2T(N/2)+O(N) => T(N)=2T(N/2)+c1N (c1为一常数) => 22T(N/22)+2c1N => ...... => 2kT(1)+kcN (N/2k=1 => k=log2N) => c2N+c1Nlog2N
综上,T(N)=O(NlogN) (不写底是因为换底只需除以一个常数,不影响复杂度规模)
标签:
原文地址:http://www.cnblogs.com/eniac12/p/4817286.html