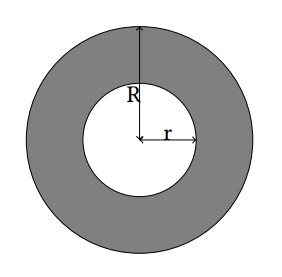
For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.
//qscqesze
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <bitset>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 1000006
#define mod 1001
#define eps 1e-9
#define PI acos(-1)
const double EP = 1E-10 ;
int Num;
//const int inf=0x7fffffff;
const ll inf=999999999;
inline ll read()
{
ll x=0,f=1;char ch=getchar();
while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
return x*f;
}
//*************************************************************************************
struct Circle{
double x,y;
double r;
};
double calArea(Circle c1, Circle c2)
{
double d;
double s,s1,s2,s3,angle1,angle2,temp;
d=sqrt((c1.x-c2.x)*(c1.x-c2.x)+(c1.y-c2.y)*(c1.y-c2.y));
if(d>=(c1.r+c2.r))//两圆相离
return 0;
if((c1.r-c2.r)>=d)//两圆内含,c1大
return acos(-1.0)*c2.r*c2.r;
if((c2.r-c1.r)>=d)//两圆内含,c2大
return acos(-1.0)*c1.r*c1.r;
angle1=acos((c1.r*c1.r+d*d-c2.r*c2.r)/(2*c1.r*d));
angle2=acos((c2.r*c2.r+d*d-c1.r*c1.r)/(2*c2.r*d));
s1=angle1*c1.r*c1.r;s2=angle2*c2.r*c2.r;
s3=c1.r*d*sin(angle1);
s=s1+s2-s3;
return s;
}
int main()
{
int t;
scanf("%d",&t);
for(int cas = 1;cas <= t;cas++)
{
Circle a1,a2,b1,b2;
double R,r;
scanf("%lf%lf",&a1.r,&a2.r);
b1.r=a1.r;
b2.r=a2.r;
scanf("%lf%lf",&a1.x,&a1.y);
scanf("%lf%lf",&b1.x,&b1.y);
a2.x=a1.x;
a2.y=a1.y;
b2.x=b1.x;
b2.y=b1.y;
double ans = 0;
ans += calArea(a1,b1);
ans -= calArea(a1,b2);
ans -= calArea(b1,a2);
ans += calArea(a2,b2);
printf("Case #%d: %.6lf\n",cas,ans);
}
}