算法导论专题一--排序算法

标签：style   blog   http   color   使用   strong   

排序算法作为许多程序的中间步骤，是计算机科学中的一个基本操作。

一、问题描述

    排序算法输入的是n个数的一个序列<a1,a2…..an>,输出为输入的一个排列<a1’,…..an’>,满足a1’<a2’<….<an’

简言之就是输入一个序列，输出的是这个数组元素从小到大排列的另一序列。

二、方法思想综述

   从算法导论这本书上根据算法的复杂度可以将排序算法分为三种，，。,这两种方法都需要数据间的比较，而不需要。

其中有三种为选择，冒泡，插入。

    选择排序：最直观，简单但是时间复杂度高，其比较次数多。思想是首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

    冒泡排序：也是相对简单的方法，其交换次数多。思想是比较序列的相邻两个元素，如果递减，后小于前，那么交换两元素。让小的元素不断的向上浮到第一个位置，然后从剩余的元素里在浮出最小的元素到第二个位置，以此类推。

    插入排序：适用用于少量元素的排序（通常为8个或以下）。思想是在已排好序的序列中找到位置，插入，初始时默认第一张是已经排好序的。这就相当于我们玩斗地主的时候，从底牌里不断抽牌，整理手牌的过程。

    其中有三种为归并，堆，快速。其中归并和快速排序都采用了分治的思想，而堆排序使用了特殊的数据结构堆进行管理。分治策略里的关键是递归，要想实现递归就要将原问题分解成类似于原问题但规模更小的子问题。

    其中有三种为计数，基数，桶。这些排序算法的特点是不需要比较操作，利用的是序列的序号和序列值之间的操作

三、过程代码分析

    选择排序：输入一个length=n的数组，从0到n-2，对于未排序的找出最小的与当前的交换。

void selection_sort(int *a, int len)
{
     int i, j, min, t;
    for(i = 0; i < len - 1; i ++)
    {
        min = i;
        //查找最小值
        for(j = i + 1; j < len; j ++)
            if(a[j]> a[min])
               min = j;
        //交换
        if(min != i)
        {
            t = a[min];
            a[min] = a[i];
            a[i] = t;
        }
    }
}

注意点1.外层循环是从0-n-2，确定了n-1个数的序列，最后一个数的也就确定了。

         2.没有记录最小元素，而是记录最小元素的下标。可以改为记录最小元素。

         3.是在第二重循环，找到最小元素后而且最小元素不是当前元素情况下才进行交换的。

例子如[3 5 8 9 10 2 1 25]

        [1 5 8 9 10 2 3 25]

.....   [1 2 3 5 8 9 10 25]

初始定最小元素下标为0，从1-n-1，如果元素值比最小元素的小，记录其下标使其而为最小元素。这里先是5后是6，循环结束后，把这个最小的和下标0这个位置的元素交换。这样经过第一次后，最小的元素就到第一个位置了。接着就定最小的元素下标为1，类推。

冒泡排序：不断把最小元素上浮，类似也可以把最大元素下沉。

注意点1.外层循环是从0-n-2，确定了n-1个数的序列，最后一个数的也就确定了。

         2.内层循环里是从n-1-i，最后一个元素到未排序的第一个元素即第i个元素。

例子如[3 5 8 9 10 2 1 25]

        [1 3 5 8 9 10 2 25]

.....   [1 2 3 5 8 9 10 25]

首先指向最后一个元素len-1，25，25<1，不交换，然后向上指向len-2，1，1<2,交换。不断的向上直到未排序的那个。这样最小元素就到了i的位置。

插入排序：

一堆牌，牌面朝下在桌面，取出第一张，一张就认为是排好序的，再从其中取出第二张，第二张跟手中已有排好序的比较，小于就继续，直到大于或者是元素超出手上的牌了。

void insertion_sort(int *a, int len)
 {
      int i, j, key;
    for(i = 1; i < len ; i ++)
    {
        key=a[i];
        j=i-1;
        while(j>=0&&a[j]>key)
        {
            a[j+1]=a[j];
            j--;
        }
        a[j+1]=key;
    }
 }

注意点1.默认第一张是排好序的，所以从第二个元素开始。

         2.在比较过程中，while循环用来实现把比key小的元素向后移动

例子如[3 5 8 9 10 2 1 25]，5 8 9 10都比3大，不符合while条件元素都不移动，所以在i=5的时候，我们已经有排好序的[5 8 9 10]手牌，这时key=2<a[j]=10，于是把10元素赋值到2的位置，而2我们已经用key来保存不会丢失。接着向上移动一个位置比较9<2，符合，赋值到后面一个位置，直到不小于key后者到顶的时候。出循环，把key值插入到正确位置。

四、算法分析

选择排序：

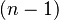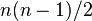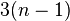    选择排序的交换操作介于和次之间。选择排序的比较操作为次之间。选择排序的赋值操作介于和次之间。

比较次数，比较次数与关键字的初始状态无关，总的比较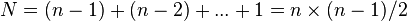次数。交换次数，最好情况是，已经有序，交换0次；最坏情况是，逆序，交换次。交换次数比冒泡排序较少，由于交换所需CPU时间比比较所需的CPU时间多，值较小时，选择排序比冒泡排序快。

原地操作几乎是选择排序的唯一优点，实际适用的场合非常罕见。

冒泡排序：

   对个项目需要O()的比较次数，且可以原地排序。尽管这个算法是最简单了解和实作的排序算法之一，但它对于少数元素之外的数列排序是很没有效率的。

冒泡排序是与插入排序拥有相等的执行时间，但是两种法在需要的交换次数却很大地不同。在最好的情况，冒泡排序需要次交换，而插入排序只要最多交换。冒泡排序的实现（类似下面）通常会对已经排序好的数列拙劣地执行（），而插入排序在这个例子只需要个运算。

插入排序：

   如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需(n-1)次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数减去(n-1)次。平均来说插入排序算法复杂度为O(n²)

参考资料：http://zh.wikipedia.org/wiki/

下节分析：归并，堆，快速

算法导论专题一--排序算法,布布扣,bubuko.com

算法导论专题一--排序算法

标签：style   blog   http   color   使用   strong   

原文地址：http://www.cnblogs.com/dawnminghuang/p/3847988.html