流形学习笔记

标签：

• 维数约简

1. 特征选择，依据某一标准选择性质最突出的特征
2. 特征抽取，经已有特征的某种变换获取约简特征

增加特征数：

1. 可以增加信息量，进而提高准确度
2. 增加训练分类器的难度，进而带来维数灾难。

解决办法：

　　选取尽可能多的、可能有用的特征，然后根据需要进行特征约简。

• 主成分分析（PCA）

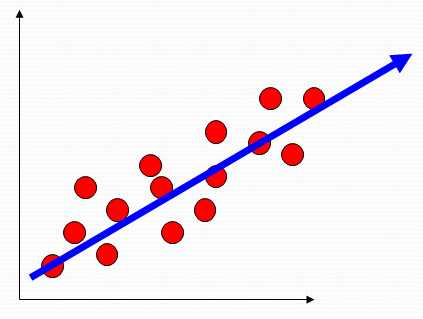
目的：

　　寻找能够表示采样数据的最好投影子空间。

求解：

　　对样本的散布矩阵（scatter matrix）进行特征值分解，所求之空间为过样本均值，（何为过样本均值？）

以最大特征值所对应的特征向量为方向的之空间。

特点：

1. 对椭球状分布的样本集具有很好的效果，理论上，学习到的主方向就是椭圆的主轴方向。
2. 非监督学习算法，能找到很好地代表所有样本的方向，但是，对于分类未必是最有利的，如下图：　　

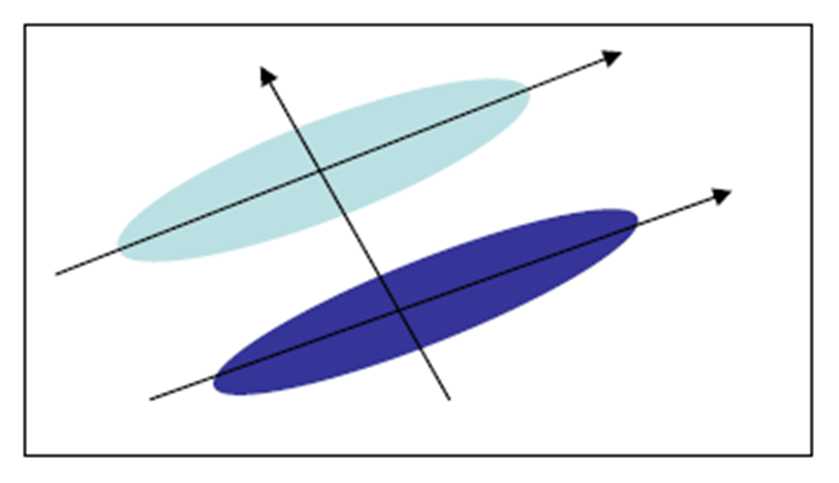
线性判别分析（LDA）

思想：

　　寻找最能把两类样本分开的投影直线

特点：

　　监督的维数约简

目标：

　　是投影后两类样本的均值之差与投影样本的总类散步的比值最大。

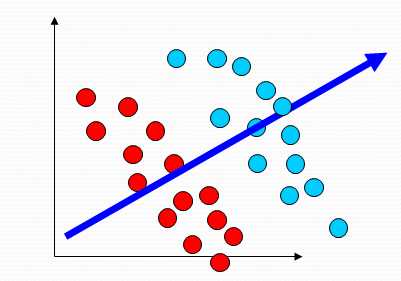
求解：

　　把原问题转化为关于样本集总类内散步矩阵和总类间散步矩阵的广义特征值问题。

• 多重判别分析（MDA）

　　LDA往多类情况的推广

　　解法与LDA类似，对于C－类问题，把样本投影到C－１维之空间。

线性方法的缺点：

线性方法对于某些数据不能进行有效的处理，这类数据，在现实中，往往很多。比如下图：

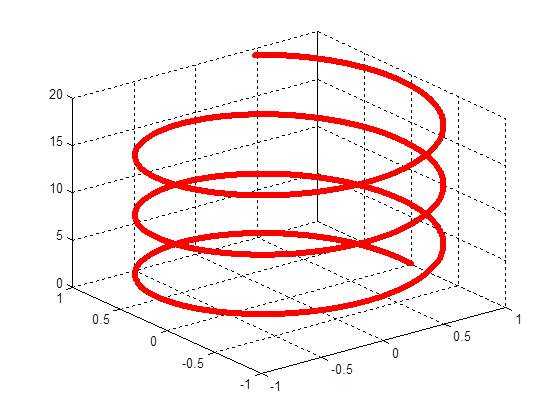
另外，现实中的数据往往并不是特征的线性组合。

比如　paper：A Global Geometric Framework　for Nonlinear Dimensionality　Reduction　所提到的人脸模型

• 流形学习

1. 是线性之空间的一种非线性推广；
2. 一种局部可坐标话的拓扑空间结构；
3. 一种非线性额维数约简方法。

可行性分析：

1. 许多高维采样数据都是由少数几个隐含变量所决定的, 如人脸采样由光线亮度, 人离相机的距离, 人的头部姿势, 人的脸部肌肉等因素决定；
2. 从认知心理学的角度来看, 心理学家认为人的认知过程是基于认知流形和拓扑连续性的。

几种经典的流形学习方法：

　　局部线性嵌入（LLE）　Nonlinear dimensionality reduction by locally linear embedding. Science

　　等距映射（IsoMap）A global geometric framework for nonlinear dimensionality reduction. Science,

　　拉普拉斯特征映射（Laplacian　Eigenmap）Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Computation,

参考：

1. 自动化所　流形学习　课件。
2. paper：A Global Geometric Framework　for Nonlinear Dimensionality　Reduction，　ｓｃｉｅｎｃｅ，２０００

流形学习笔记

标签：

原文地址：http://www.cnblogs.com/time-hummer/p/4820503.html