老师布置的几道作业

标签：

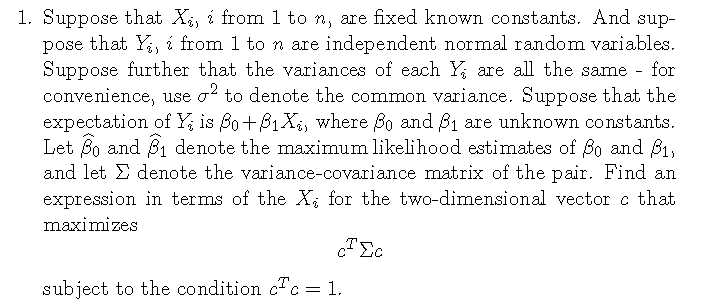
 这题问的问题 据我的理解应该是 找到使这个式子最大化的c， 用Xi表示出来， 解法我认为应该用拉格朗日乘数法。

令 $L(c,\lambda)=c^T\Sigma c - \lambda (c^Tc-1)$，然后对$L$求c的偏导数并设为0：

$$\nabla(L)_c=2\Sigma c - 2\lambda c=0$$

我们有$\Sigma c=\lambda c$，这是题目中给的式子取到极值的条件，也就是说，拉格朗日乘子是协方差矩阵的特征值，而c是对应的特征向量。

把$\Sigma c=\lambda c$代入原题，有 $$c^T\Sigma c=\lambda c^Tc$$，又因为$c^Tc=1$，因此$$c^T\Sigma c=\lambda c^Tc=\lambda$$

那么现在一切都明朗了，只要令$\lambda$等于$\Sigma$最大的特征值就可以了。

老师布置的几道作业

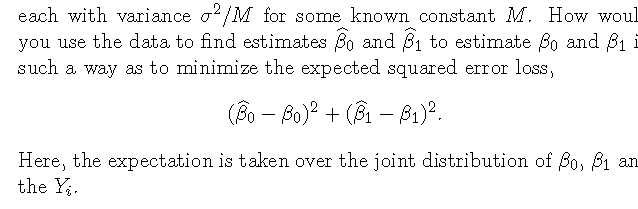
标签：

原文地址：http://www.cnblogs.com/wacc/p/4823883.html