标签:
Dinic算法:
层次图:根据源点到该点的距离建图,这里设相邻的都差1。
(下面部分转)
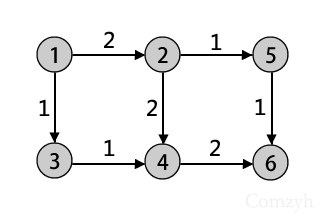
在这幅图中我们首先要增广1->2->4->6,这时可以获得一个容量为2的流,但是如果不建立4->2反向弧的话,则无法进一步增广,最终答案为2,显然是不对的,然而如果建立了反向弧4->2,则第二次能进行1->3->4->2->5->6的增广,最大流为3.
Comzyh对反向弧的理解可以说是”偷梁换柱“,请仔细阅读:在上面的例子中,我们可以看出,最终结果是1->2->5->6和1->2->4->6和1->3->4->6.当增广完1->2->4->5(代号A)后,在增广1->3->4->2->5->6(代号B),相当于将经过节点2的A流从中截流1(总共是2)走2->5>6,而不走2->4>6了,同时B流也从节点4截流出1(总共是1)走4->6而不是4->2->5->6,相当于AB流做加法.
1.bfs构建层次图。
2.dfs找从源点到汇点的路径,获得这条路径的流量I,根据这个流量修改整个图的流量(包括反向流量);
3.不断重复2,直到dfs找不到新的路径,结束;
4.重复1直到无法构成层次图为止。
#include<stdio.h> #include<string.h> #include<queue> #define maxn 210 #define LL long long using namespace std; LL map[maxn][maxn]; int n,dis[maxn]; int min(int x,int y) {return x<y?x:y;} int bfs() { int i,j; queue<int>q; memset(dis,-1,sizeof(dis)); dis[1]=0; q.push(1); while(!q.empty()) { int t=q.front(); q.pop(); for(i=1;i<=n;i++) { if(dis[i]<0&&map[t][i]) { dis[i]=dis[t]+1; q.push(i); } } } if(dis[n]>0)// 能够到达汇点,表面还能够建分层图,还能够增广。 return 1; return 0; } int dfs(int u,int low)//low表示增广路上的最小值 { int i,j,a; if(u==n)//找到汇点 return low; for(i=1;i<=n;i++) { if(map[u][i]&&dis[i]==dis[u]+1)//相连并且差一个分层距离 { a=dfs(i,min(low,map[u][i]));//找增广路 if(!a)continue;// map[u][i]-=a;//找到增广,那正向减去增广的流量 map[i][u]+=a;//反向弧增加 return a; } } return 0; } int main() { int i,j,m; while(scanf("%d%d",&m,&n)!=EOF) { memset(map,0,sizeof(map)); for(i=0;i<m;i++) { int x,y,z; scanf("%d%d%d",&x,&y,&z); map[x][y]+=z; } LL ans=0; while(bfs())//不断bfs构建分层图直到无法构建为止 { while(1)//不断dfs寻找增广路,直到无法增广为止 { int ret=dfs(1,999999999); if(!ret) break; ans+=ret; } } printf("%d\n",ans); } }
标签:
原文地址:http://www.cnblogs.com/sweat123/p/4825838.html