codeforces 446C DZY Loves Fibonacci Numbers（数学 or 数论+线段树）

时间：2014-07-16 16:45:19 阅读：418 评论：0 收藏：0 [点我收藏+]

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation

F1 = 1; F2 = 1; Fn = Fn - 1 + Fn - 2 (n > 2).

DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a1, a2, ..., an. Moreover, there are mqueries, each query has one of the two types:

Format of the query "1 l r". In reply to the query, you need to add Fi - l + 1 to each element ai, where l ≤ i ≤ r.
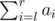Format of the query "2 l r". In reply to the query you should output the value of $bubuko.com,布布扣$ modulo 1000000009 (109 + 9).

Help DZY reply to all the queries.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000). The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — initial array a.

Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.

Output

For each query of the second type, print the value of the sum on a single line.

题目大意：维护一个序列，每次给一段序列加上一个斐波那契数列，或者询问一段序列的和。

思路1：两个斐波那契的定理，用数学归纳法很容易证明：

①定义F[1] = a, F[2] = b, F[n] = F[n - 1] + F[n - 2]（n≥3）。有F[n] = b * fib[n - 1] + a * fib[n - 2]（n≥3），其中fib[i]为斐波那契数列的第 i 项。

②定义F[1] = a, F[2] = b, F[n] = F[n - 1] + F[n - 2]（n≥3）。有F[1] + F[2] + …… + F[n] = F[n + 2] - b。

这题还有一个事实，就是两个上述定义的数列，相加，仍然符合F[n] = F[n - 1] + F[n - 2]的递推公式。

利用这两个定理，用线段树维护序列，线段树的每个结点记录这一段的前两项是什么，预处理好斐波那契数列，便能O(1)地计算出每一个结点中间的数是多少、每一个结点的和。

代码（1513MS）：

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 #include <cstdio>
 5 #include <cmath>
 6 using namespace std;
 7 typedef long long LL;
 8 #define ll (x << 1)
 9 #define rr ((x << 1) | 1)
10 #define mid ((l + r) >> 1)
11 
12 const int MOD = 1e9 + 9;
13 
14 const int MAXN = 300010;
15 const int MAXT = MAXN << 2;
16 
17 int f1[MAXT], f2[MAXT], sum[MAXT];
18 int a[MAXN], fib[MAXN];
19 int n, m;
20 
21 void init() {
22     fib[1] = fib[2] = 1;
23     for(int i = 3; i <= n + 2; ++i) {
24         fib[i] = fib[i - 1] + fib[i - 2];
25         if(fib[i] >= MOD) fib[i] -= MOD;
26     }
27 }
28 
29 int get_fib(int a, int b, int n) {
30     if(n == 1) return a;
31     if(n == 2) return b;
32     return (LL(b) * fib[n - 1] + LL(a) * fib[n - 2]) % MOD;
33 }
34 
35 int get_sum(int a, int b, int n) {
36     return (get_fib(a, b, n + 2) - b + MOD) % MOD;
37 }
38 
39 void add_fib(int x, int l, int r, int a, int b) {
40     (f1[x] += a) %= MOD;
41     (f2[x] += b) %= MOD;
42     (sum[x] += get_sum(a, b, r - l + 1)) %= MOD;
43 }
44 
45 void pushdown(int x, int l, int r) {
46     add_fib(ll, l, mid, f1[x], f2[x]);
47     add_fib(rr, mid + 1, r, get_fib(f1[x], f2[x], mid + 1 - l + 1), get_fib(f1[x], f2[x], mid + 2 - l + 1));
48     f1[x] = f2[x] = 0;
49 }
50 
51 void maintain(int x) {
52     sum[x] = (sum[ll] + sum[rr]) % MOD;
53 }
54 
55 void build(int x, int l, int r) {
56     if(l == r) {
57         sum[x] = a[l];
58     } else {
59         build(ll, l, mid);
60         build(rr, mid + 1, r);
61         maintain(x);
62     }
63 }
64 
65 void update(int x, int l, int r, int a, int b) {
66     if(a <= l && r <= b) {
67         add_fib(x, l, r, fib[l - a + 1], fib[l + 1 - a + 1]);
68     } else {
69         pushdown(x, l, r);
70         if(a <= mid) update(ll, l, mid, a, b);
71         if(mid < b) update(rr, mid + 1, r, a, b);
72         maintain(x);
73     }
74 }
75 
76 int query(int x, int l, int r, int a, int b) {
77     if(a <= l && r <= b) {
78         return sum[x];
79     } else {
80         int ret = 0;
81         pushdown(x, l, r);
82         if(a <= mid) (ret += query(ll, l, mid, a, b)) %= MOD;
83         if(mid < b) (ret += query(rr, mid + 1, r, a, b)) %= MOD;
84         return ret;
85     }
86 }
87 
88 int main() {
89     scanf("%d%d", &n, &m);
90     for(int i = 1; i <= n; ++i) scanf("%d", &a[i]);
91     init();
92     build(1, 1, n);
93     int op, l, r;
94     while(m--) {
95         scanf("%d%d%d", &op, &l, &r);
96         if(op == 1) update(1, 1, n, l, r);
97         if(op == 2) printf("%d\n", query(1, 1, n, l, r));
98     }
99 }

View Code

思路2：按官方题解的说法，有通项公式fib[n] = sqrt(5) / 5 * (((1 + sqrt(5)) / 2) ^ n - ((1 - sqrt(5)) / 2) ^ n)。

5是1e9+9的二次剩余，383008016^2=5(mod 1e9+9)。

利用逆元，可计算出：sqrt(5) / 5、(1 + sqrt(5)) / 2、(1 - sqrt(5)) / 2在模1e9+9意义下的值。

然后，变成用线段树维护两个等比数列。预处理出(1 + sqrt(5)) / 2和(1 - sqrt(5)) / 2的1~n的次方的值，设他们为q，还要求出1-q的逆元（用于计算等比数列的和）。

线段树每个结点记录两个等比数列的首项，跟上面的方法差不多，也是这样维护一个线段树即可。

代码（1996MS）：

  1 #include <iostream>
  2 #include <algorithm>
  3 #include <cstring>
  4 #include <cstdio>
  5 #include <cmath>
  6 using namespace std;
  7 typedef long long LL;
  8 #define ll (x << 1)
  9 #define rr ((x << 1) | 1)
 10 #define mid ((l + r) >> 1)
 11 
 12 const int MOD = 1e9 + 9;
 13 const int SQRT5 = 383008016;
 14 
 15 const int MAXN = 300010;
 16 const int MAXT = MAXN << 2;
 17 
 18 int powa[MAXN], powb[MAXN];
 19 int coe, ta, tb, invta, invtb;
 20 int fa[MAXT], fb[MAXT], sum[MAXT];
 21 int a[MAXN];
 22 int n, m;
 23 
 24 int inv(int x) {
 25     if(x == 1) return 1;
 26     return (LL(MOD - MOD / x) * inv(MOD % x)) % MOD;
 27 }
 28 
 29 void init() {
 30     coe = inv(SQRT5);
 31     ta = (LL(1 + SQRT5) * inv(2)) % MOD;
 32     tb = (LL(1 - SQRT5 + MOD) * inv(2)) % MOD;
 33     invta = inv(1 - ta + MOD);
 34     invtb = inv(1 - tb + MOD);
 35     //cout<<coe<<endl<<ta<<endl<<tb<<endl;
 36     powa[0] = powb[0] = 1;
 37     for(int i = 1; i <= n; ++i) {
 38         powa[i] = LL(powa[i - 1]) * ta % MOD;
 39         powb[i] = LL(powb[i - 1]) * tb % MOD;
 40     }
 41 }
 42 
 43 void maintain(int x) {
 44     sum[x] = (sum[ll] + sum[rr]) % MOD;
 45 }
 46 
 47 void add_fib(int x, int l, int r, int a, int b) {
 48     (fa[x] += a) %= MOD;
 49     (fb[x] += b) %= MOD;
 50     (sum[x] += LL(a) * (1 - powa[r - l + 1] + MOD) % MOD * invta % MOD) %= MOD;
 51     (sum[x] -= LL(b) * (1 - powb[r - l + 1] + MOD) % MOD * invtb % MOD) %= MOD;
 52     if(sum[x] < 0) sum[x] += MOD;
 53 }
 54 
 55 void pushdown(int x, int l, int r) {
 56     add_fib(ll, l, mid, fa[x], fb[x]);
 57     add_fib(rr, mid + 1, r, LL(fa[x]) * powa[mid + 1 - l] % MOD, LL(fb[x]) * powb[mid + 1 - l] % MOD);
 58     fa[x] = fb[x] = 0;
 59 }
 60 
 61 void build(int x, int l, int r) {
 62     if(l == r) {
 63         sum[x] = a[l];
 64     } else {
 65         build(ll, l, mid);
 66         build(rr, mid + 1, r);
 67         maintain(x);
 68     }
 69 }
 70 
 71 void update(int x, int l, int r, int a, int b) {
 72     if(a <= l && r <= b) {
 73         add_fib(x, l, r, LL(coe) * powa[l - a + 1] % MOD, LL(coe) * powb[l - a + 1] % MOD);
 74     } else {
 75         pushdown(x, l, r);
 76         if(a <= mid) update(ll, l, mid, a, b);
 77         if(mid < b) update(rr, mid + 1, r, a, b);
 78         maintain(x);
 79     }
 80 }
 81 
 82 int query(int x, int l, int r, int a, int b) {
 83     if(a <= l && r <= b) {
 84         return sum[x];
 85     } else {
 86         int ret = 0;
 87         pushdown(x, l, r);
 88         if(a <= mid) (ret += query(ll, l, mid, a, b)) %= MOD;
 89         if(mid < b) (ret += query(rr, mid + 1, r, a, b)) %= MOD;
 90         return ret;
 91     }
 92 }
 93 
 94 int main() {
 95     scanf("%d%d", &n, &m);
 96     for(int i = 1; i <= n; ++i) scanf("%d", &a[i]);
 97     init();
 98     build(1, 1, n);
 99     int op, l, r;
100     while(m--) {
101         scanf("%d%d%d", &op, &l, &r);
102         if(op == 1) update(1, 1, n, l, r);
103         if(op == 2) printf("%d\n", query(1, 1, n, l, r));
104     }
105 }

View Code

codeforces 446C DZY Loves Fibonacci Numbers（数学 or 数论+线段树）,布布扣,bubuko.com

codeforces 446C DZY Loves Fibonacci Numbers（数学 or 数论+线段树）

标签：des style blog http color os

原文地址：http://www.cnblogs.com/oyking/p/3848682.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行