标签:
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 4267 | Accepted: 2003 |
Description
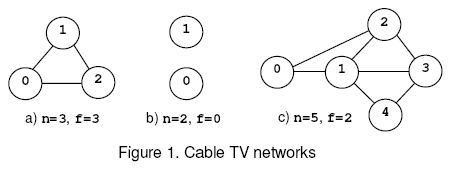
Input
Output
Sample Input
0 0 1 0 3 3 (0,1) (0,2) (1,2) 2 0 5 7 (0,1) (0,2) (1,3) (1,2) (1,4) (2,3) (3,4)
Sample Output
0 1 3 0 2
Hint
Source

图的连通度问题是指:在图中删去部分元素(点或边),使得图中指定的两个点s和t不连通 (不存在从s到t的路径),求至少要删去几个元素。
图的连通度分为点连通度和边连通度:
(1)点连通度:只许删点,求至少要删掉几个点(当然,s和t不能删去,这里保证原图中至少有三个点);
(2)边连通度:只许删边,求至少要删掉几条边。
并且,有向图和无向图的连通度求法不同,因此还要分开考虑(对于混合图,只需将其中所有的无向边按照
无向图的办法处理、有向边按照有向图的办法处理即可)。
【1】有向图的边连通度:
这个其实就是最小割问题。以s为源点,t为汇点建立网络,原图中的每条边在网络中仍存在,容量为1,求该网络的最小割(也就是最大流)的值即为原图的边连通度。
【2】有向图的点连通度:
需要拆点。建立一个网络,原图中的每个点i在网络中拆成i‘与i‘‘,有一条边<i‘, i‘‘>,容量为1 (<s‘, s‘‘>和<t‘, t‘‘>例外,容量为正无穷)。原图中的每条边<i, j>在网络中为边<i‘‘, j‘>,
容量为正无穷。以s‘为源点、t‘‘为汇点求最大流,最大流的值即为原图的点连通度。
说明:最大流对应的是最小割。显然,容量为正无穷的边不可能通过最小割,也就是原图中的边和s、t两个点不能删去;若边<i, i‘‘>通过最小割,则表示将原图中的点i删去。
【3】无向图的边连通度:
将图中的每条边(i, j)拆成<i, j>和<j, i>两条边,再按照有向图的办法(【1】)处理;
【4】无向图的点连通度:
将图中的每条边(i, j)拆成<i, j>和<j, i>两条边,再按照有向图的办法(【2】)处理。
关键就是建图,然而我并不懂为什么这样建。。。

#include <cstdio> #include <iostream> #include <sstream> #include <cmath> #include <cstring> #include <cstdlib> #include <string> #include <vector> #include <map> #include <set> #include <queue> #include <stack> #include <algorithm> using namespace std; #define ll long long #define _cle(m, a) memset(m, a, sizeof(m)) #define repu(i, a, b) for(int i = a; i < b; i++) #define repd(i, a, b) for(int i = b; i >= a; i--) #define sfi(n) scanf("%d", &n) #define pfi(n) printf("%d\n", n) #define sfi2(n, m) scanf("%d%d", &n, &m) #define pfi2(n, m) printf("%d %d\n", n, m) #define pfi3(a, b, c) printf("%d %d %d\n", a, b, c) #define MAXN 105 #define V 55 const int INF = 0x3f3f3f3f; int edge[V][V]; int N,M; int n,m; #define maxn 210 const int inf = 0x3f3f3f3f; struct EK { int cap[maxn][maxn]; int flow[maxn][maxn]; int n; void init(int n) { this->n = n; memset(cap, 0, sizeof(cap)); } void addCap(int i, int j, int val) { cap[i][j] = val; } int solve(int source, int sink) { if(source == sink) return inf;///源=汇, 流量无穷大! static int que[maxn], pre[maxn], d[maxn]; ///bfs时的队列; bfs时某点的前驱; 增光路径的流量 int p, q, t;///bfs时的队列底、顶; bfs时当前元素 memset(flow, 0, sizeof(flow)); while(true) { memset(pre, 255, sizeof(pre)); d[source] = inf; p = q = 0; que[q ++] = source; while(p<q && pre[sink]==-1) { t = que[p ++]; for(int i = 0; i < n; i ++) //注意下标 { if(pre[i]==-1 && cap[t][i]-flow[t][i]>0) { ///残余=cap-flow pre[i] = t; que[q++]=i; d[i] = min(d[t], cap[t][i]-flow[t][i]); } } } if(pre[sink]==-1) break;///没有增广路径了! for(int i = sink; i != source; i = pre[i]) { flow[pre[i]][i] += d[sink]; flow[i][pre[i]] -= d[sink]; } } t = 0;///当做网络流量 for(int i = 0; i < n; i ++) t += flow[source][i]; return t; } }ek; char s[105]; //void init() //{ // _cle(vis, 0); // _cle(pre, 0); // _cle(anc, 0); // _cle(deg, 0); // _cle(edge, 0); //} int main() { int n, m; while(~sfi2(n, m)) { //init(); _cle(edge, 0); ek.init(2 * n); repu(i, 0, m) { scanf("%s", s); int x = 0, y = 0; if(s[2] == ‘,‘) { x = s[1] - ‘0‘; if(s[4] == ‘)‘) y = s[3] - ‘0‘; else y = (s[3] - ‘0‘) * 10 + s[4] - ‘0‘; } else { x = (s[1] - ‘0‘) * 10 + s[2] - ‘0‘; if(s[5] == ‘)‘) y = s[4] - ‘0‘; else y = (s[4] - ‘0‘) * 10 + s[5] - ‘0‘; } edge[x][y] = edge[y][x] = 1; //pfi2(x, y); } //repu(i, 0, n) pfi2(i, deg[i]); repu(i, 0, n) ek.addCap(i, i + n, 1); repu(i, 0, n) repu(j, 0, n) if(edge[i][j]) ek.addCap(i + n, j, inf); int minn = n, ans; repu(i, 0, n) repu(j, 0, n) { ek.addCap(i, i + n, inf); ek.addCap(j, j + n, inf); ans = ek.solve(i, j); ek.addCap(i, i + n, 1); ek.addCap(j, j + n, 1); //pfi(ans); minn = min(ans, minn); } pfi(minn); } return 0; }
标签:
原文地址:http://www.cnblogs.com/sunus/p/4828630.html