标签:
机器学习笔记(一)
今天正式开始机器学习的学习了,为了激励自己学习,也为了分享心得,决定把自己的学习的经验发到网上来让大家一起分享。
贝叶斯学习
先说一个在著名的MLPP上看到的例子,来自于Josh Tenenbaum 的博士论文,名字叫做数字游戏。
用我自己的话叙述就是:为了决定谁洗碗,小明和老婆决定玩一个游戏。小明老婆首先确定一种数的性质C,比如说质数或者尾数为3;然后给出一系列此类数在1至100中的实例D= {x1,...,xN} ;最后给出任意一个数x请小明来预测x是否在D中。如果小明猜错了就要去洗碗,当然,如果猜对了就下饭馆吃。
举个例子,当D={16, 8, 2, 64},小明会猜测发起者给出的C是2的n次方或者偶数的形式,因此如果x=32时,小明马上会很确定答案应该是YES。是但如果x是10的话,小明可能会稍微有些犹豫了。不过幸运的是,小明是个码农,贝叶斯学习的算法给小明提供了一个判断的工具。它基本的思想是最终的概率(后验概率)正比于似然概率(likelihood)和先验概率(prior)的乘积
(1)似然概率
在此例中,再假设均匀取样时,很明显似然概率由以下公式给出:
![]()
即样本空间越大,取到某一个特定集合的概率越小。
(2)先验概率
先验概率代表着对似然概率的一种补充。他可以由历史资料得出,也可以由经验来得出。在此例中,假如D = {16,8,2,64},那么小明可以得到两种可能的h。一个是2的n次方,另一个是2的n次方除去32。如果只考虑似然概率的话,后一种情况的概率明显更大,但由生活经验我们可以知道除非老婆非常变态,否则不太可能出第二种那么道德沦丧的集合。因此我们给予“正常”的集合相对大的先验概率,“不正常”的反之,使得最终的结果更加符合我们的经验。
(3)后验概率
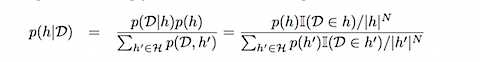
基本的贝叶斯公式相信大家都很清楚了。使用的时候由于分母是定值,因此只要判定分子就可以了。即先验概率和似然概率的乘积
下图是具体的展示。
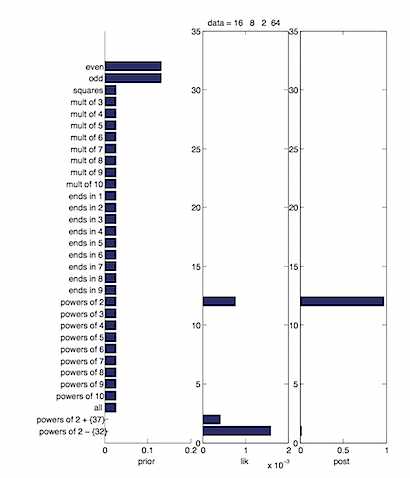
可以看到即使第二种假设的似然概率更大,但是后验概率是第一种更大,这是符合大家的经验的。
(可惜的是,这个故事的结果是后一种假设正确,小明又愉快地去洗碗了)
先验概率的加入可以使我们应对“黑天鹅事件”的发生,具体的数学解释会在下一篇文章中阐述。
标签:
原文地址:http://www.cnblogs.com/cklwanfifa/p/4830582.html