标签:
1、前言
中学甚至是小学,了解方程的时候,我们一定是学习过高斯消元法的,或许当时只是不是这种称呼罢了。而这个知识点,在信息学上依旧可以运用,甚至有着更多的推广的功能。
2、方程转矩阵
我们先从最简单的求解三元一次方程入手。现存在一个方程组,我们将其写成一个矩阵:
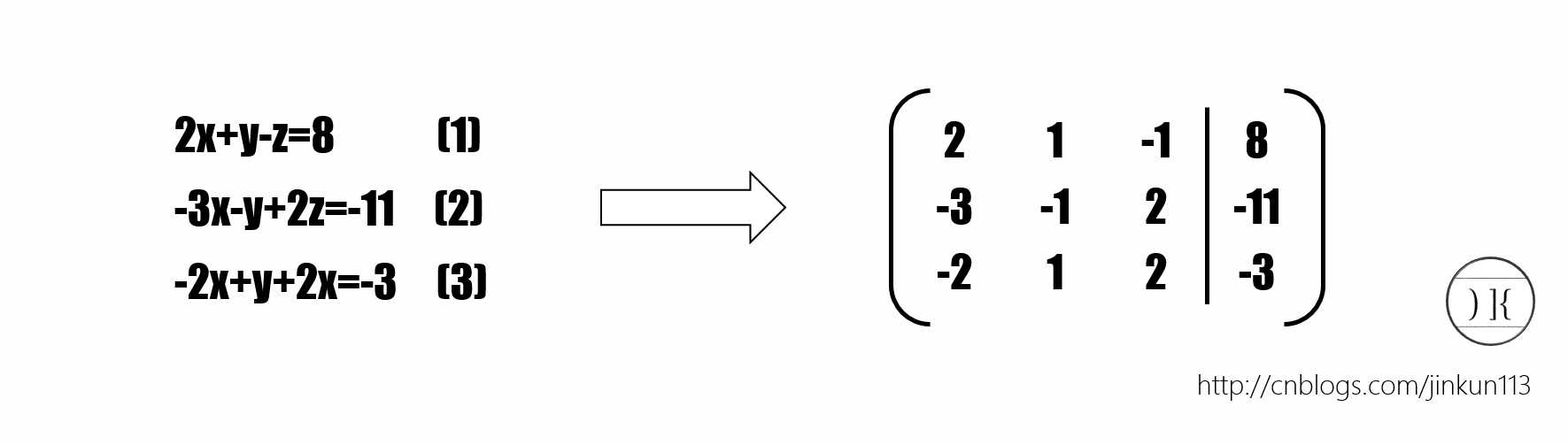
这个矩阵我们称之为增广矩阵(Augmented Matrix)。左侧部分为系数矩阵,最后一列是等号右边的常数列。为什么要把他转换为矩阵,因为这更加符合信息学的制式,我们直接拿二维数组存下来就行了。三元一次方程组还是很好解的,我们借用下当年的解方程方法就可以轻松地理解这些过程。
我们固然知道,解三元一次方程组,需要进行两次消元。推广到一般的,对于n元一次,需要进行n-1次消元,我们的步骤就是从第1行起一行行处理,直至n-1行,使最终对于第i行,a[i][i]!=0 && a[j][i]==0 (j>i)。为了提高数值稳定性,每次消元之前,对于第i行,我们需要从第i+1行至第n行选取一行,设其为第x行,存在绝对值最大的a[x][i],然后交换第x行和第i行。不要问我为什么,我也不清楚提高数值稳定性具体是个什么概念,只可意会,不可言传。
3、加减消元
消元的核心步骤。依旧是上面那个例子。从第1行起处理,第一步我们找到了第2行满足所述条件,将其与第1行交换,得:
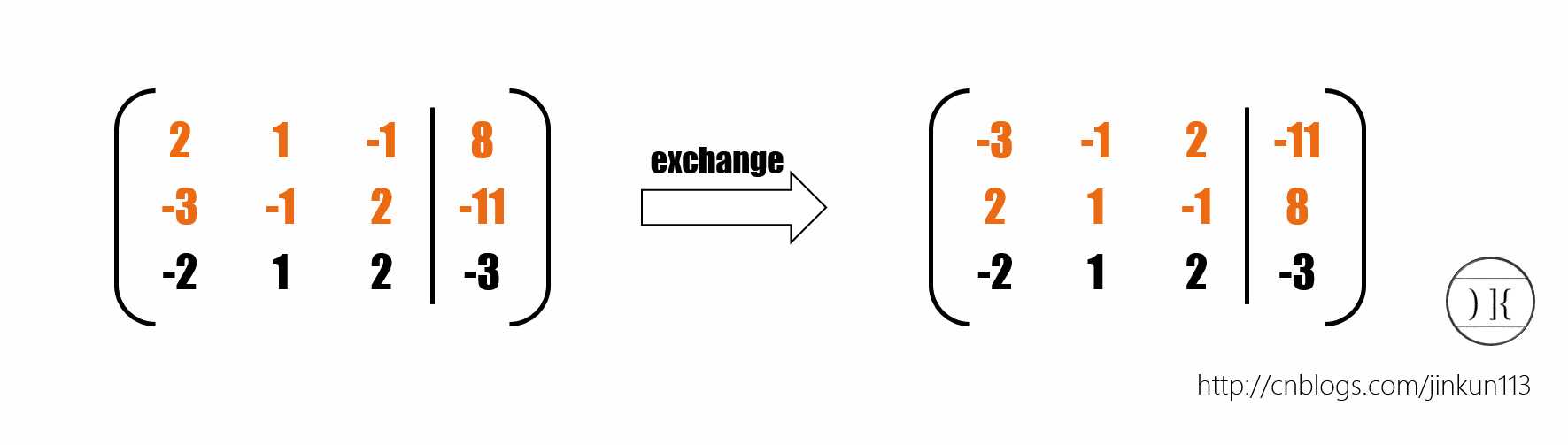
然后{-3,-1,2,-11}就成为当前行了。根据当前行,依次将后面所有的行的第1位通过加减进行消除。例如第2行每个元素*(-3/2),然后与第1行相加得到{0,1/3,1/3,2/3}。
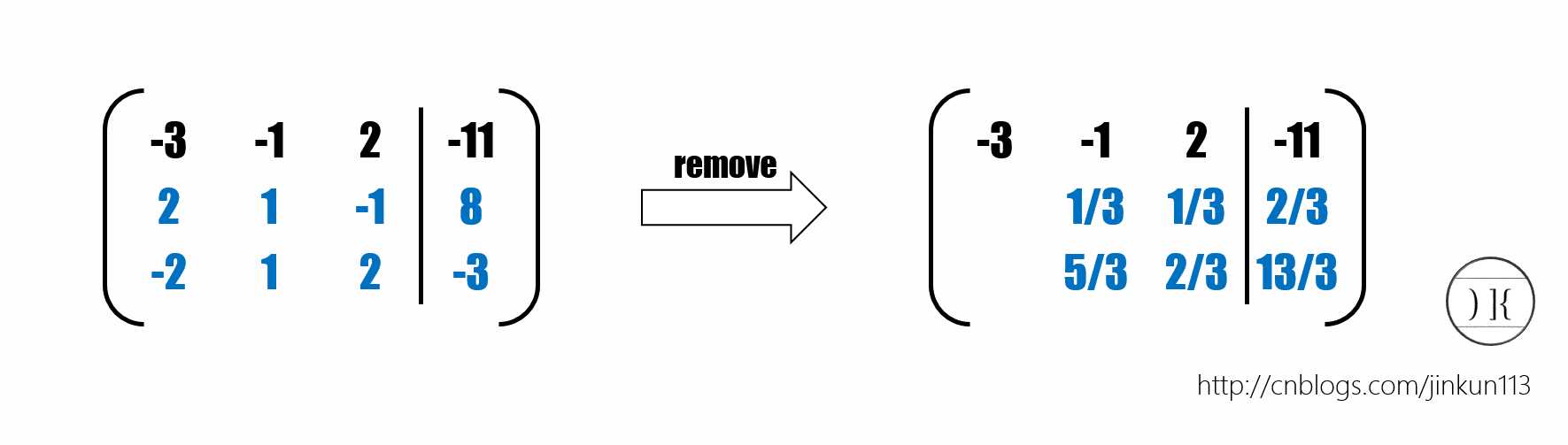
推广到一般情况,即用第i行消去第j行的第i列,那么第j行的第k列有a[j][k]-=a[j][i]/a[i][i],其中j∈(i+1,n),k∈(i,n+1)。
在一步步的消除之后,对于第n行,必定仅存在一个系数矩阵元素。例如还是上述例子,消元结束后,最后一列元素为{0,0,1/5,-1/5},即z/5=-1/5 => z=-1。而将z代入上一行,可以得到y=3;将y,z的值代入上一行,可以得到x=2。这个步骤我们称之为回代。
代码(消元+回代):
----------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------
标签:
原文地址:http://www.cnblogs.com/jinkun113/p/4830769.html