标签:
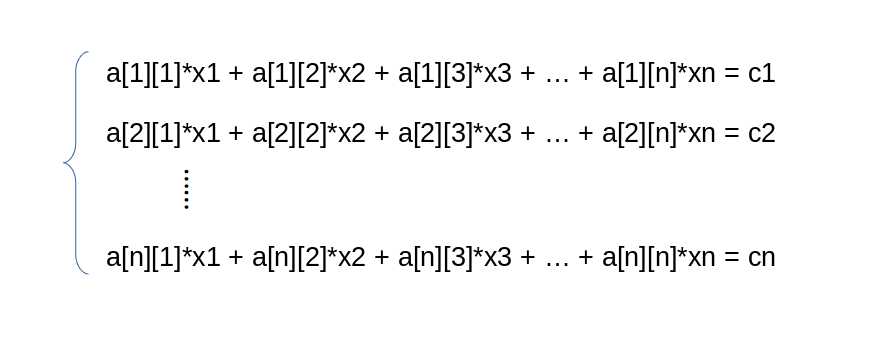
如果遇到这种解方程的题目,想把它每个未知数写出公式可不容易,而在不知道解的数据范围的时候,二分枚举什么的和没做没区别,所以这里引入了高斯消元对此进行解答。
高斯消元简直就是为计算机量身打造的解n元一次方程组的利器,虽然在算法竞赛中并不会考像加减消元这种容易的题目,但是这作为它的基础,还是需要讨论一下的。
1、基础概念
高斯消元是指,用第i个式子将它下方的n-i个式子的第i个未知数系数通过加减消元法变为零,然后反过来求解所有未知数的过程。
2、加减消元
为了方便描述,我们将每个式子按照同一个未知数对齐的原则进行排列(若有的方程中有的未知数不存在,则系数用0表示,即空位),并且把未知数都放在左边,常数放在右边,为了简化写法,这里用行列式表示每个方程中各个未知数的系数,图中第i行第j列表示的是第i个方程第j个未知数的系数,第n+1列表示的是常数项(为了方便描述,假定所有的系数都不为零,为零的情况稍候讨论),如下描述:
a[1][1] a[1][2] a[1][3] ... a[1][n] | c[1]
a[2][1] a[2][2] a[2][3] ... a[2][n] | c[2]
. .
. .
. .
a[n][1] a[n][2] a[n][3] ... a[n][n] | c[n]
然后进行第一步操作:
a[1][1] a[1][2] a[1][3] ... a[1][n] | c[1]
0 a[2][2]*a[1][1]-a[1][2]*a[2][1] a[2][3]*a[1][1]-a[1][3]*a[2][1] ... | c[2]*a[1][1]-c[1]*a[2][1]
0 a[3][2]*a[1][1]-a[1][2]*a[3][1] a[3][3]*a[1][1]-a[1][3]*a[3][1] ... | c[3]*a[1][1]-c[1]*a[3][1]
. .
. .
上图很清晰得表达了我们操作的意义,经过第一步操作,除了第一个方程之外,所有方程第一项的系数都变成了0,更新每个方程的系数。而接下来的第二步则使得除了第一,二个方程之外的第二项系数变成了0,如此反复,直至第n-1步之后,你会惊奇的发现,第n个方程中只有第n个未知数了!而那就是一个一元一次方程!很容易得到了x[n]的值,接下来将x[n]n代入上面的每一个方程,并将其与常数项合并,你又会发现,x[n-1]也可以通过第n-1个方程求解了!如此逆推而上,就得到了所有未知数的值!
3、算法分析
通过上述的解法,很容易就可以敲出代码,但是还有要注意的地方:
No.1 无解的情况:
当有一个方程所有系数都为0而常数项不为0时,方程组是无解的;
No.2 有系数为零的情况:
在处理数据的过程中,可能遇到某个系数为零,这时是可以直接跳过的,因为我们在这一步上的目的即使跳过它了也能完成。
下面是详细代码:
#include<cstdio> const int maxn = 100 + 10; //假设要求解的方程组最多为100元 double dat[maxn][maxn],ans[maxn]; //整数除法可能会出问题(万一不能整除呢?) int n; bool rt = 1; //记录是否有解 void init() { //初始化,读入式子中的系数 scanf("%d",&n); for(int i = 1;i <= n;++ i){ for(int j = 1;j <= n + 1;++ j){ scanf("%lf",&dat[i][j]); } } } void work() { //处理所得到的数据 for(int i = 1;i <= n;++ i){ int j = i; while(dat[j][i]==0) j ++; //防止某些式子有的部分系数为零,这时使用j下方第一个dat[j][i]不为零的式子来更新它下面的式子 for(int k = j+1;k <= n + 1;++ k){ for(int m = i;m <= n + 1;++ m){ dat[k][m] = dat[k][m]*dat[j][i] - dat[j][m]*dat[k][i]; } } } if(dat[n+1][n+1]) rt = 0; //若所有系数都为零而等式右边不为零时,方程组无解 } void solv() { if(!rt) return; for(int i = n;i >= 1;-- i){ //从下往上求解 if(dat[i][i] == 0) continue; ans[i] = dat[i][n+1]/dat[i][i]; for(int j = i-1;j >= 1;-- j){ dat[j][n+1] -= dat[j][i]*ans[i]; } } } void prnt() { //输出答案 if(!rt) {printf("No Answer!");return;} for(int i = 1;i <= n;++ i){ printf("x%d ",i); if(ans[i] != (1<<30)){ printf("= %.2lf",ans[i]); } else{ printf("is unknown"); } printf("\n"); } } int main(){ init(); //初始化 work(); //处理数据 solv(); //求解 prnt(); //输出 return 0; }
版权声明:本文为博主原创文章,未经博主允许不得转载。
标签:
原文地址:http://www.cnblogs.com/woodenhead/p/4833493.html