标签:
写在最前: 对最近的工作进行简要总结,毕竟老了,容易忘。 力求言简意赅,了解思想,不过分深入算法。
这里有两个链接大家参考:
1. https://www.youtube.com/watch?v=HMGX8HXskKk
2. http://blog.csdn.net/zouxy09/article/details/8532111
简介:
Graph cuts 也叫图割(复数), 所以从字面上就一个图(图论里的图)可以有多个割,这里的割,指分割,也就是segmetation。 算法的含义就是用图论(graph)的方法对图像(image)进行分割,边缘提取。
正文:
Step 1: 建立图, 从图像到图的的建立。

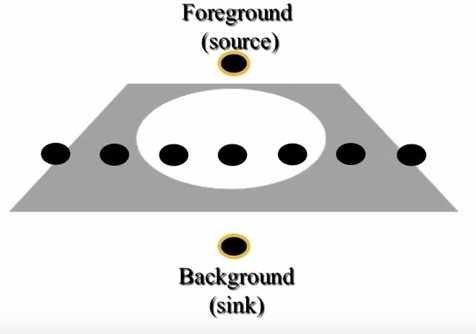
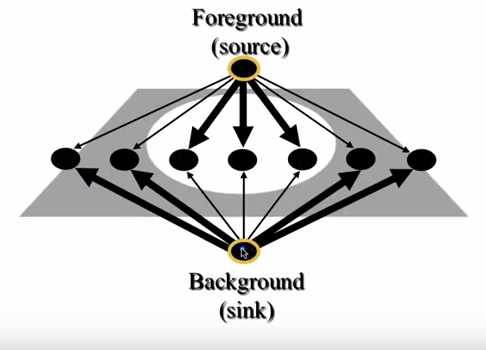
顶点:图像的每个像素(注意是每个像素)作为图中的顶点,也叫第一类顶点;第二类顶点是为了图割算法而引入的,叫sourse和sink 分别对应S和T,图的顶点建立完毕。
边: 图的顶点之间的链接,也就是边。两种顶点建立两种边:第一种边是第一类顶点之间的链接,叫做n-links;第二种边是第二类顶点和第一类顶点之间的边,叫t-links。
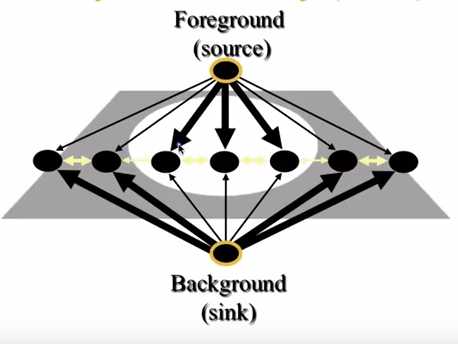
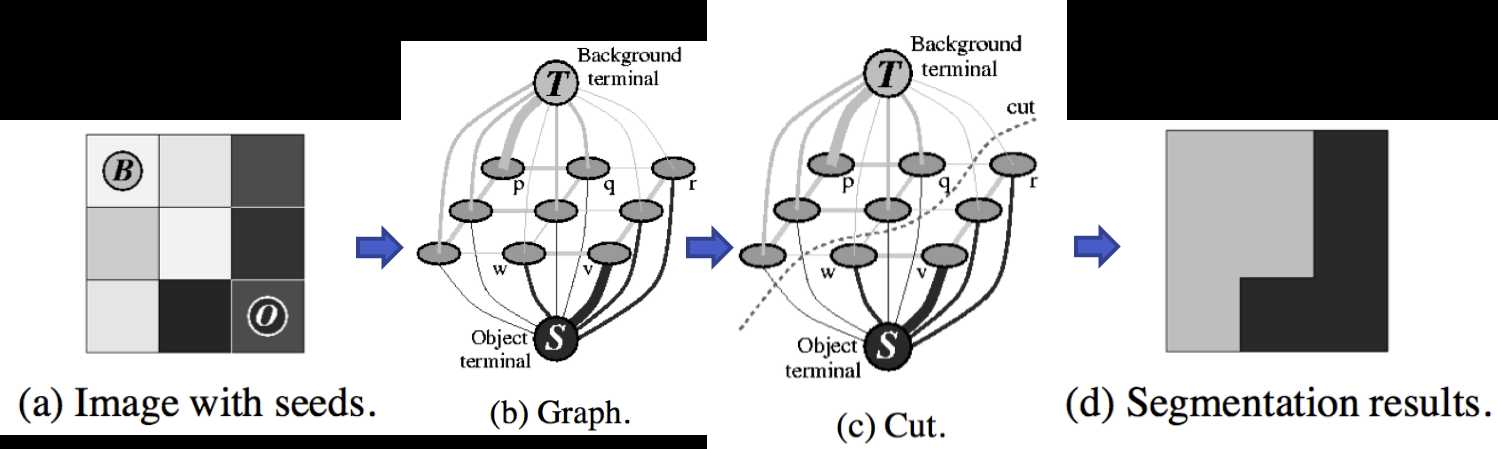
step 2: 分割,引入图论中的min cut(最小割),顾名思义,让整个图分割时所付出的代价最小,也就是损失函数的加权和最小。 所以图的边还需要权重(损失函数),从上图中我们发现有的边粗,有的边细,他们就代表了边的权重。 如何设计损失函数(边的权重)?
第一类边(n-links)的权是像素相似性的度量,general的想法就是:像素之间的相似性,相似性越大,权重越大,相似性越小,权重越小,我们通过切断相似性小的边,达到图像分割的目的,使前景和背景分开。
第二类边(t-links)的权重如何定义呢? 简单来说,graph cuts需要用户的预先定义两个点,就是S和T,所以,我们至少知道两个分别属于前景和背景的点,那么两个点周围各自的点,属于该前景或背景的概率就会很大,我们甚至可以预先定义一些前景点和背景点作为算法的输入。
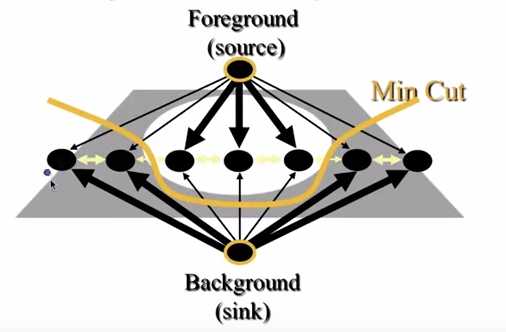
通过min cut 算法,得到了这个图像的分割。 要求1:分割可以把图中的顶点分为互不相交的两个集合。要求2:损失最小。 这个分割是穿过t-links和n-links的。 同时我们就得到图像的分割(segmentation)。
整个流程的图示2:
数学:
第一类边的权重(也叫区域项):
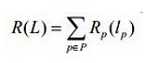
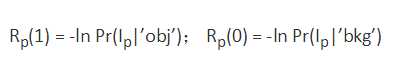
第二类边的权重(也叫边界项):
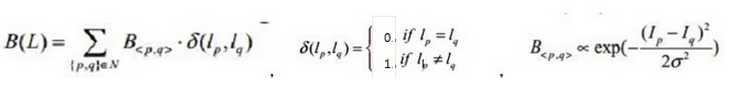
图像的能量表示,min cut就是求这个能量最小:
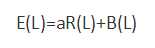
标签:
原文地址:http://www.cnblogs.com/Matrix420/p/4839248.html