标签:
题意:
给出平面直角坐标系上的n个点的坐标,表示一个多边形蛋糕,先判断是否是凸多边形,若否,输出"I can‘t cut."。若是,则对这个蛋糕进行3角形剖分,切n-3次变成n-2份三角形蛋糕给小伙伴吃,但是每切一次需要一个费用,公式是:cost[i][j] = |xi + xj| * |yi + yj| % p 表示在两点i和j之间切一刀的费用。问最少费用是多少?
思路:
判断是否凸多边形需要用到求凸包的Andrew算法,时间复杂度为O(nlogn),然后判断凸包内的点数是否为n就行了。(大白书p271)
求最小费用需要用到分治的一些思想,当然主要还是dp。
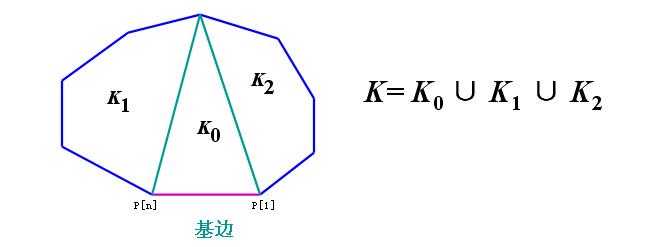
如下图的凸多边形(图来自这里),如果点1和点n还差1个点就成为三角形了,我们可以枚举这个点k,切两刀,取出K0(不能再切),变成K1和K2两块,以刚切的1->k和k->n这两条边为基边,继续分治切下去,直到剩下1个三角形为止。那么以edge[i][j]为基边来切开这个子凸多边形的费用是dp[i][j]=max(dp[i][j], dp[i][k]+dp[i][k]+cost[i][k]+cost[k][j]),所有点对的cost可以先求出来。注意在计算dp[i][j]时,dp[i][k]和dp[k][j]必须先求出来。

1 //#include <bits/stdc++.h> 2 #include <iostream> 3 #include <cstdio> 4 #include <cstring> 5 #include <cmath> 6 #include <map> 7 #include <deque> 8 #include <algorithm> 9 #include <vector> 10 #include <iostream> 11 #define pii pair<int,int> 12 #define max(x,y) ((x)>(y)?(x):(y)) 13 #define min(x,y) ((x)<(y)?(x):(y)) 14 #define abs(x) ((x)<0?-(x):(x)) 15 #define INF 0x3f3f3f3f 16 #define LL long long 17 using namespace std; 18 const double PI = acos(-1.0); 19 const int N=500; 20 21 struct node 22 { 23 int x,y; 24 node(){}; 25 node(int x,int y):x(x),y(y){}; 26 }Po[N], path[N]; 27 int n, p, c[N][N], dp[N][N]; 28 29 30 inline int cmp(node a,node b) 31 { 32 if(a.x==b.x) return a.y<b.y; 33 return a.x<b.x; 34 } 35 inline int cross(node A,node p1,node p2) //叉积,A是新来的点。若A在p1->p2左边,则结果为正。 36 { 37 return (p1.x-A.x)*(p2.y-A.y) - (p2.x-A.x)*(p1.y-A.y); 38 } 39 int get_cost(node a,node b){return abs(a.x+b.x)*abs(a.y+b.y)%p;} //在a和b之间切开的费用 40 41 int ConvexHull(node *u,int n,node *path) //求凸包,返回凸包中的点数 42 { 43 sort(u,u+n,cmp); //先按x再按y排序 44 int top=0; 45 for(int i=0; i<n; i++) //下凸包:从左到右 46 { 47 while(top>1 && cross(u[i],path[top-1],path[top-2])<=0 ) top--; //小于0,在右边 48 path[top++]=u[i]; 49 } 50 int k=top; 51 for(int i=n-2; i>=0; i--) //上凸包:从右到左 52 { 53 while(top>k && cross(u[i],path[top-1],path[top-2])<=0 ) top--; 54 path[top++]=u[i]; 55 } 56 if(n>1) top--; //起点是重复了的,要去掉 57 return top; 58 } 59 60 61 62 int cal() 63 { 64 if(n==3) return 0; //3点则0费用 65 memset(c,0,sizeof(c)); 66 for(int i=0; i<n; i++) //任意两点间连一条边的费用c 67 for(int j=i+2; j<n; j++) 68 c[i][j]=c[j][i]=get_cost( path[i], path[j] ); 69 for(int i=0; i<n; i++) 70 { 71 for (int j=0; j<n; j++) dp[i][j]=INF; 72 dp[i][i+1] = 0; //相邻两个点不能连线,可视为费用为0. 73 } 74 for(int j=2; j<n; j++) //升序 75 { 76 for(int i=j-2; i>=0; i--) //降序 77 { 78 for(int k=i+1; k<j; k++) //枚举三角形顶点 79 dp[i][j]=min(dp[i][j], dp[i][k]+dp[k][j]+c[i][k]+c[k][j]); 80 } 81 } 82 return dp[0][n-1]; 83 } 84 85 int main() 86 { 87 //freopen("input.txt", "r", stdin); 88 while(~scanf("%d%d",&n,&p)) 89 { 90 for(int i=0; i<n; i++) scanf("%d%d",&Po[i].x,&Po[i].y); 91 if(ConvexHull(Po,n,path)<n) puts("I can‘t cut."); 92 else printf("%d\n", cal()); 93 } 94 95 return 0; 96 }
标签:
原文地址:http://www.cnblogs.com/xcw0754/p/4839359.html